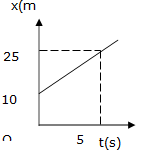Một xe khối lượng 2 tấn, bắt đầu chuyển động nhanh dần đều từ A trên đ

Câu hỏi
Nhận biếtMột xe khối lượng 2 tấn, bắt đầu chuyển động nhanh dần đều từ A trên đường nằm ngang AB dài 20 m. Lực kéo của động cơ không đổi là F = 5200 N. Hệ số ma sát trên mặt đường ngang là 0,1. Lấy g = 10 m/s2. (Giải bài toán bằng cách dùng các định luật bảo toàn)
a) Tính vận tốc của xe tại B.
b) Đến B, xe tắt máy và đi lên dốc nghiêng góc 180 so với phương ngang. Bỏ qua ma sát. Tìm quãng đường tối đa xe đi được trên dốc.
c) Đến B, xe tắt máy và đi lên dốc nghiêng góc 180 so với phương ngang. Hệ số ma sát trên mặt dốc là 0,2. Tìm quãng đường tối đa xe đi được trên dốc.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Tóm tắt:
\(\begin{array}{l}
m = 2T = 2000{\rm{ }}kg\\
F = 5200N;S = 20m\\
\mu = 0,1;g = 10{\rm{ }}m/{s^2}
\end{array}\)
a) Tính vận tốc ở cuối đường.
b) Đến B, xe tắt máy và đi lên dốc nghiêng góc 180 so với phương ngang. Bỏ qua ma sát. Tìm quãng đường tối đa xe đi được trên dốc
c) Đến B, xe tắt máy và đi lên dốc nghiêng góc 180 so với phương ngang. Hệ số ma sát trên mặt dốc là 0,2. Tìm quãng đường tối đa xe đi được trên dốc.
Bài làm:
a) Áp dụng định lý động năng:
\(\frac{1}{2}.m.{v^2} - \frac{1}{2}.m.v_0^2 = {A_{ms}} + {A_{Fk}}\,\,\,\left( {{v_0} = 0} \right)\)
Ta có:
\(\begin{array}{l}
\frac{1}{2}.m.{v^2} - \frac{1}{2}.m.v_0^2 = {A_{ms}} + {A_{Fk}}\\
\Rightarrow \frac{1}{2}.m.{v^2} = \mu .m.g.s + F.s\\
\Rightarrow \frac{1}{2}.2000.{v^2} = - 0,1.2000.10.20 + 5200.20 \Rightarrow v = 8\left( {m/s} \right)
\end{array}\)
Vậy vB = 8 m/s.
b) Áp dụng định lý động năng ta có:
\(0 - \frac{1}{2}.m.{v^2} = - m.g.S.\sin \alpha \Rightarrow {S_{\max }} = 10,{36_{}}m\)
c) Áp dụng định lý động năng ta có:
\(\begin{array}{l}
- \frac{1}{2}.m.{v^2} = - m.g.S.\sin \alpha - \mu .m.g.S.sin\alpha \\
\Rightarrow - \frac{1}{2}{.2000.8^2} = - 2000.10.S.\sin {18^0} - 0,2.2000.10.S.\sin {18^0}\\
\Rightarrow {S_{\max }} = 6,{41_{}}m
\end{array}\)
Luyện tập
Câu hỏi liên quan
-

Phương trình của một vật chuyển động thẳng có dạng: x = -3t + 4 (m; s). Kết luận nào sau đây đúng

Một ngừơi đi xe đạp trên 2/3 đoạn đừơng đầu với vận tốc trung bình 10km/h và 1/3 đoạn đừơng sau với vận tốc trung bình 20km/h. Vận tốc trung bình của ngừơi đi xe đạp trên cả quảng đừơng là

Một xe chuyển động thẳng không đổi chiều có vận tốc trung bình là 20Km/h trên 1/4 đoạn đường đầu và 40Km/h trên 3/4 đoạn đường còn lại. Vận tốc trung bình của xe trên cả đoạn đường là :

Một xe chuyển động thẳng không đổi chiều; 2 giờ đầu xe chạy với vận tốc trung bình 60km/h, 3 giờ sau xe chạy với vận tốc trung bình 40km/h. Vận tốc trung bình của xe trong suốt thời gian chạy là:

Phương trình chuyển động của một chất điểm dọc theo trục Ox có dạng : x = 5 + 60t (x : m, t đo bằng giờ).Chất điểm đó xuất phát từ điểm nào và chuyển động với vận tốc bằng bao nhiêu ?

Một vật chuyển động thẳng không đổi chiều. Trên quãng đường AB, vật đi nửa quãng đường đầu với vận tốc v1 = 20m/s, nửa quãng đường sau vật đi với vận tốc v2 = 5m/s. Vận tốc trung bình trên cả quãng đường là:

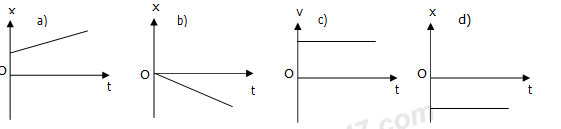
Trên hình là đồ thị tọa độ-thời gian của một vật chuyển động
thẳng.
Cho biết kết luận nào sau đây là sai?


Một vật chuyển động thẳng không đổi chiều trên 1 quãng đường dài 40m. Nửa quãng đường đầu vật đi hết thời gian t1 = 5s, nửa quãng đường sau vật đi hết thời gian t2 = 2s. Tốc độ trung bình trên cả quãng đường là:

Một vật chuyển động thẳng đều với vận tốc v = 2 m/ s. Và lúc t = 2 s thì vật có toạ độ x = 5 m. Phương trình toạ độ của vật là