Cho đường tròn ( O ) tâm O, đường kính AB và C là điểm nằm trên đoạn t

Câu hỏi
Nhận biếtCho đường tròn \(\left( O \right)\) tâm \(O\), đường kính \(AB\) và \(C\) là điểm nằm trên đoạn thẳng \(OB\) (với \(C \ne B\)). Kẻ dây \(DE\) của đường tròn \(\left( O \right)\) vuông góc với \(AC\) tại trung điểm \(H\) của \(AC\). Gọi \(K\) là giao điểm thứ hai của \(BD\) với đường tròn đường kính \(BC\).
a) Chứng minh tứ giác \(DHCK\) là tứ giác nội tiếp.
b) Chứng minh \(CE\) song song với \(AD\) và ba điểm \(E,\,\,C,\,\,K\) thẳng hàng.
c) Đường thẳng qua \(K\) vuông góc với \(DE\) cắt đường tròn \(\left( O \right)\) tại hai điểm \(M\) và \(N\) (với \(M\) thuộc cung nhỏ \(AD\)). Chứn mginh \(E{M^2} + D{N^2} = A{B^2}\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
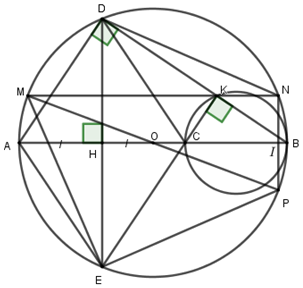
a) Chứng minh tứ giác \(DHCK\) là tứ giác nội tiếp.
Ta có: \(\angle DHB = {90^0}\) (\(DE \bot AB\) tại \(H\)) \( \Rightarrow \angle DHC = {90^0}\).
\(\angle CKB = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính \(BC\)) \( \Rightarrow \angle CKD = {90^0}\).
Xét tứ giác \(DHCK\) có \(\angle DHC + \angle CKD = {180^0}\), mà hai góc ở vị trí đối diện nên tứ giác \(DHCK\) nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)) (đpcm).
b) Chứng minh \(CE\) song song với \(AD\) và ba điểm \(E,\,\,C,\,\,K\) thẳng hàng.
Có \(DE \bot AB \Rightarrow HD = HE\) (quan hệ vuông góc giữa đường kính và dây cung).
Lại có \(HA = HC\,\,\left( {gt} \right)\) nên tứ giác \(DAEC\) là hình bình hành \( \Rightarrow CE//DA\) (đpcm).
Lại có: \(\angle CKB = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính \(BC\)) \( \Rightarrow CK \bot KB\) (1)
Mà \(\angle ADB = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính \(AB\)) \( \Rightarrow AD \bot DB\) (2)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(CK//AD\) (từ vuông góc đến song song).
Mà \(CE//AD\,\,\left( {cmt} \right)\) nên theo tiên đề Ơclit suy ra ba điểm \(E,C,K\) thẳng hàng.
c) Đường thẳng qua \(K\) vuông góc với \(DE\) cắt đường tròn \(\left( O \right)\) tại hai điểm \(M\) và \(N\) (với \(M\) thuộc cung nhỏ \(AD\)). Chứn mginh \(E{M^2} + D{N^2} = A{B^2}\).
Kẻ đường kính \(MP\) cửa đường tròn \(\left( O \right)\). Nối \(N\) với \(P\) cắt \(AB\) tại \(I\). Nối \(E\) với \(P\), \(E\) với \(B\).
Có \(\angle MNP = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow MN \bot NP\).
Mà \(MN \bot DE\,\,\left( {gt} \right)\) nên \(NP//DE\) (từ vuông góc đến song song) \( \Rightarrow DNPE\) là hình thang.
Lại có \(DE \bot AB,NP//DE \Rightarrow NP \bot AB\) \( \Rightarrow I\) là trung điểm của \(NP\) (quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow B\) là điểm chính giữa cung \(NP\).
\( \Rightarrow \) số đo cung \(NB\) bằng số đo cung \(PB\).
Dễ thấy, tam giác \(\Delta BDE\) cận tại \(B\) (đường cao \(BH\) cũng là đường trung tuyến)
\( \Rightarrow BD = BE\) \( \Rightarrow \) số đo cung \(BD\) bằng số đo cung \(BE\).
\( \Rightarrow sd\,\,cung\,\,DB - sd\,\,cung\,\,\,BN = sd\,\,cung\,\,EB - sd\,\,cung\,\,BP \Rightarrow sd\,\,cung\,\,\,DN = sd\,\,\,cung\,\,\,EP \Rightarrow DN = EP\) (hai dây căng hai cung bằng nhau thì bằng nhau).
Do đó \(E{M^2} + D{N^2} = E{M^2} + E{P^2} = M{P^2}\) (do tam giác \(\Delta MEP\) vuông tại \(E\)). Mà \(MP = AB\) (= đường kính).
Vậy \(E{M^2} + E{P^2} = A{B^2}\) (đpcm).

