Cho đoạn thẳng AB và C là điểm nằm giữa A và B. Trên cùng một nửa mặt

Lời giải của Tự Học 365

Giải chi tiết:

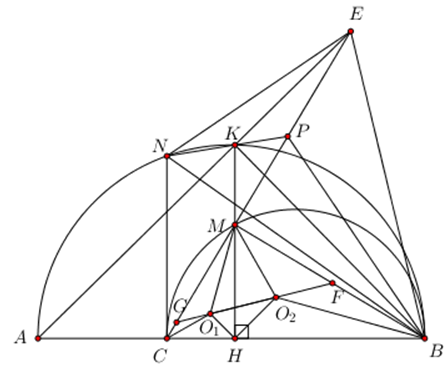
a) Ta có \(\widehat{BME}=\widehat{BKE}={{90}^{0}}\) (góc nội tiếp chắn nửa đường tròn)

\(\Rightarrow \) Hai điểm M và K cùng nhìn BE dưới 1 góc \({{90}^{0}}\Rightarrow \) Tứ giác BMKE là tứ giác nội tiếp.

\(\Rightarrow \widehat{BEC}=\widehat{BKH}\) (hai góc nội tiếp cùng chắn cung BM).

Mà \(\widehat{BKH}=\widehat{BAE}\) (cùng phụ với \(\widehat{ABK}\)) \(\Rightarrow \widehat{BEC}=\widehat{BAE}\)

Xét tam giác BEC và tam giác BAE có: \(\widehat{ABE}\) chung; \(\widehat{BEC}=\widehat{BAE}\,\,\left( cmt \right)\)

\(\Rightarrow \Delta BEC\backsim \Delta BAE\,\,\left( g.g \right)\Rightarrow \frac{BE}{BA}=\frac{BC}{BE}\Rightarrow B{{E}^{2}}=BA.BC\,\,\left( 1 \right)\)

b) Ta có \(\widehat{ANB}={{90}^{0}}\Rightarrow \Delta ANB\) vuông tại N \(\Rightarrow BC.BA=B{{N}^{2}}\,\,\left( 2 \right)\)

Từ (1) và (2) \(\Rightarrow BN=BE\Rightarrow \Delta BNE\) cân tại B \(\Rightarrow \widehat{BNE}=\widehat{BEN}\,\,\left( 3 \right)\)  và B thuộc trung trực của NE.

Ta có \(\widehat{BNP}=\widehat{BAK}\) (hai góc nội tiếp cùng chắn cung BK).

Mà \(\widehat{BAK}=\widehat{BAE}=\widehat{BEC}\,\,\left( \Delta BEC\backsim \Delta BAE \right)\Rightarrow \widehat{BNP}=\widehat{BEP}\,\,\left( 4 \right)\)

Từ (3) và (4) \(\Rightarrow \widehat{PNE}=\widehat{PEN}\Rightarrow \Delta PNE\) cân tại P \(\Rightarrow P\) thuộc trung trực của NE.

\(\Rightarrow BP\) là trung trực của NE.

Do tam giác BNE cân tại B và tam giác PNE cân tại P nên trung trực BP đồng thời là đường phân giác.

Do đó tâm đường tròn nội tiếp các tam giác BNE và PNE cùng nằm trên BP.

c) Gọi G, F lần lượt là giao điểm của O₁O₂ với MC và MB.

Ta có \(\widehat{{{O}_{1}}HM}=\widehat{{{O}_{2}}HB}={{45}^{0}}\) và \(\widehat{{{O}_{1}}MH}=\frac{1}{2}\widehat{HMC}=\frac{1}{2}\widehat{MBH}=\widehat{{{O}_{2}}BH}\)

\(\Rightarrow \Delta {{O}_{1}}HM\backsim \Delta {{O}_{2}}HB\,\,\left( g.g \right)\Rightarrow \frac{{{O}_{1}}H}{{{O}_{2}}H}=\frac{MH}{BH}\)

Ta có \(\Delta MHC\backsim BHM\,\left( g.g \right)\Rightarrow \frac{MH}{BH}=\frac{MC}{BM}\Rightarrow \frac{{{O}_{1}}H}{{{O}_{2}}H}=\frac{CM}{BM}\Rightarrow \frac{{{O}_{1}}H}{CM}=\frac{{{O}_{2}}H}{BM}\)

Vì \({{O}_{1}}H;{{O}_{2}}H\) là phân giác của hai góc kề bù \(\Rightarrow {{O}_{1}}H\bot {{O}_{2}}H\Rightarrow \widehat{{{O}_{1}}H{{O}_{2}}}={{90}^{0}}=\widehat{BMC}\)

Xét tam giác \({{O}_{1}}H{{O}_{2}}\) và \(CMB\) có  \(\widehat{{{O}_{1}}H{{O}_{2}}}=\widehat{BMC}={{90}^{0}};\,\,\frac{{{O}_{1}}H}{CM}=\frac{{{O}_{2}}H}{BM}\,\,\left( cmt \right)\Rightarrow \Delta {{O}_{1}}H{{O}_{2}}\backsim \Delta CMB\,\,\left( c.g.c \right)\)

\(\Rightarrow \widehat{{{O}_{1}}{{O}_{2}}H}=\widehat{CBM}\) (hai góc tương ứng). Mà \(\widehat{{{O}_{1}}{{O}_{2}}H}+\widehat{H{{O}_{2}}F}={{180}^{0}}\Rightarrow \widehat{CBM}+\widehat{H{{O}_{2}}F}={{180}^{0}}\Rightarrow \) Tứ giác HO₂FB là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰)

\(\Rightarrow \widehat{MFG}=\widehat{{{O}_{2}}HB}={{45}^{0}}\) (cùng bù với \(\widehat{{{O}_{2}}FB}\))

\(\Rightarrow \Delta MEG\) vuông cân tại M.

Xét tam giác MO₂H và MO₂F có :

\(\widehat{HM{{O}_{2}}}=\widehat{FM{{O}_{2}}}\,\,\left( gt \right);\,\,\widehat{MH{{O}_{2}}}=\widehat{MFG}={{45}^{0}}\,\,\left( cmt \right)\Rightarrow \widehat{M{{O}_{2}}H}=\widehat{M{{O}_{2}}F}\)

MO₂ chung

\(\Rightarrow \Delta M{{O}_{2}}H=\Delta M{{O}_{2}}F\,\,\left( g.c.g \right)\Rightarrow MH=MF;\,\,H{{O}_{2}}=F{{O}_{2}}\)

CMTT ta có \(MH=MG\) và \(H{{O}_{1}}=G{{O}_{1}}\)

\(\Rightarrow \) Chu vi tam giác \({{O}_{1}}{{O}_{2}}H\) là :

\(C=H{{O}_{1}}+H{{O}_{2}}+{{O}_{1}}{{O}_{2}}=G{{O}_{1}}+F{{O}_{1}}+{{O}_{1}}{{O}_{2}}=GF\Rightarrow \) Để chu vi tam giác O₁HO₂ lớn nhất \(\Leftrightarrow G{{F}_{\max }}\)   

Xét tam giác vuông cân MEF có \(G{{F}^{2}}=M{{G}^{2}}+M{{F}^{2}}=2M{{G}^{2}}=2M{{H}^{2}}\Rightarrow EF=MH\sqrt{2}\)

x\(\Rightarrow G{{F}_{\max }}\Leftrightarrow M{{H}_{\max }}\Leftrightarrow M\) là điểm chính giữa cung BC.