Cho hai đường tròn (O) và (O’) cắt nhau tại 2 điểm A, B (O và O’ thuộc

Câu hỏi
Nhận biếtCho hai đường tròn (O) và (O’) cắt nhau tại 2 điểm A, B (O và O’ thuộc 2 nửa mặt phẳng bờ AB). Tiếp tuyến chung gần B của 2 đường tròn lần lượt tiếp xúc với (O), (O’) tại C, D. Qua A kẻ đường thẳng song song với CD lần lượt cắt (O), (O’) tại M, N (khác A). Các đường thẳng CM và DN cắt nhau tại E. Gọi P, Q là giao điểm của MN với BC và BD. Chứng minh rằng:
a) Đường thẳng AE vuông góc với CD.
b) Tứ giác BECD nội tiếp.
Tam giác EPQ là tam giác cân
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
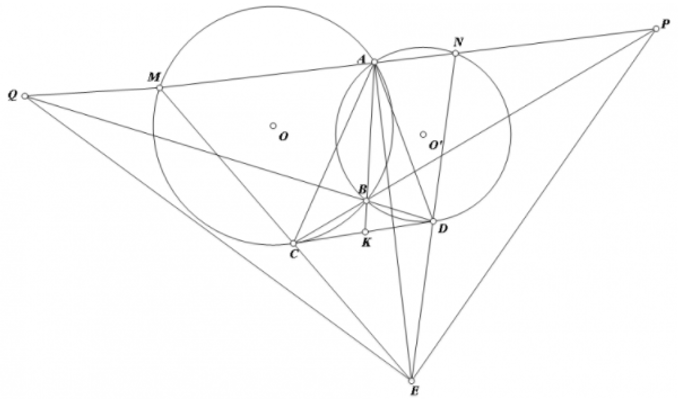
a) Ta có :
\(\widehat{ECD}=\widehat{AMC}=\widehat{ACE}\)
Chứng minh tương tự ta có : \(\widehat{CDE}=\widehat{CDA}\)
Từ đây suy ra CD là trung trực của AE.
b) Dễ thấy :
\(\begin{array}{l}
\left\{ \begin{array}{l}
\widehat {BCD} = \widehat {BAC}\\
\widehat {BDC} = \widehat {BAD}
\end{array} \right. \Rightarrow \widehat {CBD} = {180^0} - \widehat {BCD} - \widehat {BDC}\\
\Rightarrow \widehat {CBD} = {180^0} - \widehat {CAD} = {180^0} - \widehat {CED}
\end{array}\)
\(\Rightarrow BECD\) là tứ giác nội tiếp.
c) Gọi K là giao điểm của AB và CD
Nhận thấy :
\(\begin{array}{l}
\left\{ \begin{array}{l}
\Delta BCK \sim \Delta CAK \Rightarrow K{C^2} = KB.KA\\
\Delta DBK \sim \Delta ADK \Rightarrow K{D^2} = KB.KA
\end{array} \right. \Rightarrow KC = KD\\
CD//PQ \Rightarrow \frac{{KD}}{{AQ}} = \frac{{KC}}{{AP}} \Rightarrow AQ = QP
\end{array}\)
Mà \(AE\bot PQ\Rightarrow \) Tam giác EPQ cân tại E

