Cho đường tròn ( O ) có hai đường kính AB và MN vuông góc với nhau. Tr

Câu hỏi
Nhận biếtCho đường tròn \(\left( O \right)\) có hai đường kính \(AB\) và \(MN\) vuông góc với nhau. Trên tia đối của tia \(MA\) lấy điểm \(C\) khác điểm \(M\). Kẻ \(MH\) vuông góc với \(BC\) (\(H\) thuộc \(BC\)).
a) Chứng minh \(BOMH\) là tứ giác nội tiếp
b) \(MB\) cắt \(OH\) tại \(E.\) Chứng minh \(ME.HM = BE.HC.\)
c) Gọi giao điểm của đường tròn \(\left( O \right)\) và đường tròn ngoại tiếp tam giác \(MHC\) là \(K.\) Chứng minh ba điểm \(C,K,E\) thẳng hàng.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
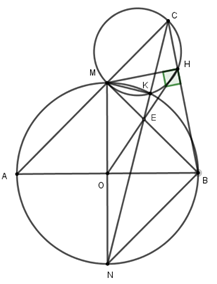
a) Chứng minh \(BOMH\) là tứ giác nội tiếp
Vì \(AB \bot MN\) tại \(O\) nên \(\angle MOB = 90^\circ \)
Vì \(MH \bot BC\) tại \(H\) nên \(\angle MHB = 90^\circ \)
Xét tứ giác \(BOMH\) có \(\angle MOB + \angle MHB = 90^\circ + 90^\circ = 180^\circ \) mà hai góc ở vị trí đối nhau nên \(BOMH\) là tứ giác nội tiếp (dhnb).
b) \(MB\) cắt \(OH\) tại \(E.\) Chứng minh \(ME.HM = BE.HC.\)
Ta có có \(AB = MN,\,AB \bot MN\) tại \(O\) nên \(MBNA\) là hình vuông
Xét tam giác \(HMB\) và tam giác \(HCM\) có
\(\angle MHB = \angle CHM = 90^\circ \) và \(\angle HMB = \angle MCH\) (cùng phụ với \(\angle CMH\))
Suy ra \(\Delta HMB \sim \Delta HCM\left( {g - g} \right)\) \( \Rightarrow \frac{{HM}}{{HB}} = \frac{{HC}}{{HM}}\) (1)
Vì tứ giác \(BOHM\) nội tiếp (theo câu a) nên \(\angle MHE = \angle OBM\) mà \(\angle OBM = 45^\circ \) (do \(MBNA\) là hình vuông)
Do đó \(\angle MHE = \angle EHB\) hay \(HE\) là phân giác \(\angle MHB\).
Xét tam giác \(MHB\) có \(HE\) là tia phân giác \(\angle MHB\) nên \(\frac{{ME}}{{EB}} = \frac{{MH}}{{HB}}\) (2)
Từ (1) và (2) suy ra \(\frac{{HC}}{{HM}} = \frac{{ME}}{{EB}} \Leftrightarrow HC.EB = MH.ME\) (đpcm)
c) Gọi giao điểm của đường tròn \(\left( O \right)\) và đường tròn ngoại tiếp tam giác \(MHC\) là \(K.\) Chứng minh ba điểm \(C,K,E\) thẳng hàng.
*) Ta chứng minh \(C,E,N\) thẳng hàng
+ Theo câu b) ta có \(HC.EB = MH.ME \Leftrightarrow \frac{{HC}}{{HM}} = \frac{{ME}}{{EB}}\) (3)
+ Xét \(\Delta MHC\) và \(\Delta BMC\) có:
\(\begin{array}{l}\angle C\,\,\,chung\\\angle MHC = \angle CMB = 90^\circ \\ \Rightarrow \Delta MCH \sim \Delta BCM\,\,\,\left( {g - g} \right)\\ \Rightarrow \frac{{HC}}{{HM}} = \frac{{CM}}{{MB}}\end{array}\)
Mà \(MB = BN\) (do \(AMBN\) là hình vuông)
\( \Rightarrow \frac{{HC}}{{HM}} = \frac{{CM}}{{BN}}\) (4)
Từ (3) và (4) suy ra \(\frac{{ME}}{{BE}} = \frac{{CM}}{{BN}} \Rightarrow \frac{{ME}}{{CM}} = \frac{{BE}}{{BN}}\)
Xét \(\Delta MEC\) và \(\Delta {\rm B}{\rm E}{\rm N}\) có \(\angle MCE = \angle NBE = 90^\circ \) và \(\frac{{ME}}{{CM}} = \frac{{BE}}{{BN}}\) (cmt) nên \(\Delta MEC \sim \Delta BEN\,\left( {c - g - c} \right)\)
Suy ra \(\angle MEC = \angle BEN\) mà \(M,E,B\) thẳng hàng nên \(C,E,N\) thẳng hàng.
*) Xét \(\left( O \right)\) có \(\angle MKN = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Vì \(\Delta MHC\) vuông tại \(H\) nên đường tròn ngoại tiếp tam giác \(MHC\) là đường tròn đường kính \(MC\)
Xét đường tròn đường kính \(MC\) có \(\angle MKC = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra \(\angle MKN + \angle MKC = 90^\circ + 90^\circ = 180^\circ \) nên ba điểm \(N,K,C\) thẳng hàng.
Lại có \(N,E,C\) thẳng hàng (cmt) nên ba điểm \(E,K,C\) thẳng hàng.

