Một dây dẫn thẳng dài vô hạn đặt trong không khí đi qua A mang dòng đ
Câu hỏi
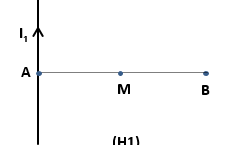
Nhận biếtMột dây dẫn thẳng dài vô hạn đặt trong không khí đi qua A mang dòng điện có cường độ I1 = 1,5A và phương, chiều như hình vẽ (H1). Biết AM = 15cm, AB = 30cm.
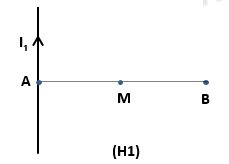
a) Tính cảm ứng từ tại diểm M.
b) Đặt dây dẫn thẳng dài vô hạn mang dòng điện I2 đi qua B song song với dây dẫn trên thì cảm ứng từ tổng hợp tại M có độ lớn 3.10-6 T . Hỏi dòng điện chạy trong dây dẫn đi qua B có chiều như thế nào và cường độ bao nhiêu?
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Tóm tắt:
\(\begin{array}{l}
{I_1} = 1,5A;AM = 15cm;AB = 30cm\\
a)\,\,{B_M} = ?\\
b)\,\,{B_M}' = {3.10^{ - 6}}T;{I_2} = ?
\end{array}\)
Bài giải:
a) Cảm ứng từ của dòng điện thẳng dài:
\({B_{1M}} = {2.10^{ - 7}}.\frac{I}{r} = {2.10^{ - 7}}.\frac{{1,5}}{{0,15}} = {2.10^{ - 6}}(T)\)
b) Áp dụng quy tắc nắm tay phải ta xác định vecto cảm ứng từ tại M do I1 gây ra: có phương vuông góc với mặt phẳng chứa dòng điện và chiều hướng vào trong.
Theo nguyên lý chồng chất từ trường thì cảm ứng từ tổng hợp tại M:
\(\overrightarrow {{B_M}} = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Mà theo ý a) thì \({B_{1M}} < {B_M}\), nên vec tơ \(\overrightarrow {{B_{2M}}} \) phải có cùng phương và cùng chiều với \(\overrightarrow {{B_{1M}}} \).
Tức là có phương vuông góc với mặt phẳng chứa dòng điện và chiều hướng vào trong.
Áp dụng quy tắc nắm tay phải ta xác định được chiều của dòng điện I2 (như hình vẽ).
Vì vec tơ \(\overrightarrow {{B_{2M}}} \) có cùng phương và cùng chiều với \(\overrightarrow {{B_{1M}}} \) nên:
\({B_M} = \left| {{B_{1M}} + {\rm{ }}{B_{2M}}} \right| \Rightarrow {B_{2M}} = {3.10^{ - 6}} - {2.10^{ - 6}} = {10^{ - 6}}T\)
Áp dụng công thức tính cảm ứng từ ta có:
\({B_{2M}} = {2.10^{ - 7}}.\frac{{{I_2}}}{{r_2^2}} \Rightarrow {I_2} = \frac{{{B_{2M}}}}{{{{2.10}^{ - 7}}}}.r_2^2 = \frac{{{{10}^{ - 6}}}}{{{{2.10}^{ - 7}}}}.0,15 = 0,75A\)
Vậy dòng điện I2 có cường độ 0,75 A và ngược chiều với dòng điện I1.
Luyện tập
Câu hỏi liên quan
-




Khi tăng nhiệt độ của một kim loại sẽ làm tăng điện trở của kim loại này, nguyên nhân gây ra hiện hượng này là:



Đặt một hiệu điện thế U không đổi vào hai cực của bình điện phân. Xét trong cùng một khoảng thời gian, nếu kéo hai cực của bình ra xa sao cho khoảng cách giữa chúng tăng gấp 2 lần thì khối lượng chất được giải phóng ở điện cực so với lúc trước sẽ:

