Cho đường tròn ( O ) đường kính AB, điểm I nằm giữa hai điểm A và

Câu hỏi
Nhận biếtCho đường tròn \(\left( O \right)\) đường kính \(AB,\) điểm \(I\) nằm giữa hai điểm \(A\) và \(O\,\,\left( {I \ne A,\,\,O} \right).\) Kẻ đường thẳng vuông góc với \(AB\) tại \(I,\) đường thẳng này cắt đường tròn \(\left( O \right)\) tại \(M\) và \(N.\) Gọi \(S\) là giao điểm của hai đường thẳng \(BM\) và \(AN,\) qua \(S\) kẻ đường thẳng song song với \(MN,\) đường thẳng này cắt các đường thẳng \(AB\) và \(AM\) lần lượt tại \(K\) và \(H.\)
1) Chứng minh rằng tứ giác \(SKAM\) nội tiếp.
2) Chứng minh rằng \(SA.SN = SB.SM\)
3) Chứng minh rằng \(KM\) là tiếp tuyến của đường tròn \(\left( O \right).\)
4) Chứng minh rằng 3 điểm \(H,\,\,B,\,\,N\) thẳng hàng.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
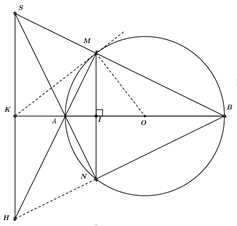
1) Chứng minh rằng tứ giác \(SKAM\) nội tiếp.
Vì \(M \in \left( {O;\,\,AB} \right) \Rightarrow \angle AMB\) là góc nội tiếp chắn nửa đường tròn
\( \Rightarrow \angle AMB = {90^0} \Rightarrow \angle SMA = {90^0}.\)
Vì \(SK\parallel MN\, \Rightarrow SK \bot AB \Rightarrow \angle SKA = {90^0}\)
Xét tứ giác \(SKAM\) có \(\angle SMA + \angle SKA = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow SKAM\) nội tiếp đường tròn (tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
2) Chứng minh rằng \(SA.SN = SB.SM\)
Ta có: \(\angle ANB\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow \angle ANB = {90^0}\)
Xét \(\Delta SMA\)và \(\Delta SNB\)có:
\(\begin{array}{l}\angle NSB\,\,\,chung\\\angle SMA = \angle SNB\,\,\left( { = {{90}^0}} \right)\\ \Rightarrow \Delta SMA \sim \Delta SNB\,\,\,\left( {g - g} \right)\\ \Rightarrow \frac{{SM}}{{SN}} = \frac{{SA}}{{SB}} \Leftrightarrow SM.SB = SA.SN\,\,\,\,\left( {dpcm} \right).\end{array}\)
3) Chứng minh rằng \(KM\) là tiếp tuyến của đường tròn \(\left( O \right).\)
Xét \(\Delta SMH\)và\(\Delta SKB\)có:
\(\begin{array}{l}\angle HSB\,\,\,chung\\\angle SMH = \angle SKB = {90^0}\\ \Rightarrow \Delta SMH \sim \Delta SKB\,\,\,\left( {g - g} \right)\\ \Rightarrow \frac{{SM}}{{SK}} = \frac{{SH}}{{SB}}\,\,\\ \Rightarrow \Delta SMK \sim \Delta SHB\,\,\,\left( {c - g - c} \right)\\ \Rightarrow \angle SMK = \angle SHB.\end{array}\)
Vì \(SN\parallel MN\)(do cùng cuông góc với \(AB\))
\( \Rightarrow \angle BMN = \angle BSH\)(hai góc đồng vị)
Xét \(\left( O \right)\) đường kính \(AB\) có \(\angle MNB = \angle MAB\) (cùng chắn cung \(MB\) )
\(\Delta AMO\)cân tại \(O\) (vì có \(OM = OA\)) nên \(\angle AMO = \angle MAB\)
\(\begin{array}{l} \Rightarrow \angle AMO = \angle SMK\\ \Rightarrow \angle AMO + \angle KMH = \angle SMK + \angle KMH\\ \Rightarrow \angle SMH = \angle KMO = {90^0}\\ \Rightarrow KM \bot OM\end{array}\)
\( \Rightarrow KM\) là tiếp tuyến của \(\left( O \right)\) (đpcm).
4) Chứng minh rằng 3 điểm \(H,\,\,B,\,\,N\) thẳng hàng.
Theo câu 3 ta chứng minh được \(\frac{{SM}}{{SK}} = \frac{{SH}}{{SB}}\)
\(\begin{array}{l} \Rightarrow SM.SB = SH.SK\\ \Rightarrow SH.SK = SA.SN\,\left( { = SM.SB} \right)\\ \Rightarrow \Delta SKA \sim \Delta SNH\\ \Rightarrow \angle SKA = \angle SNH = {90^0}\end{array}\)
Lại có \(\angle HNB = \angle HNS + \angle SNB = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow H,\,\,N,\,\,B\) thẳng hàng (đpcm).

