Cho tam giác ABC có ba góc nhọn và AB < BC < AC, kẻ hai đường cao AM v

Câu hỏi
Nhận biếtCho tam giác ABC có ba góc nhọn và \(AB < BC < AC\), kẻ hai đường cao AM và BN cắt nhau tại H \(\left( {M \in BC,\,\,N \in CA} \right)\).
a) Chứng minh tứ giác CMHN nội tiếp.
b) Chứng minh \(NA.NC = NH.NB\)
c) Đường tròn tâm H bán kính HA cắt các tia AB, AC lần lượt tại E, F \(\left( {E \ne A;\,\,F \ne A} \right)\). Chứng minh tứ giác BHFC nội tiếp.
d) Các tiếp tuyến tại E và F của đường tròn \(\left( {H;HA} \right)\) cắt nhau tại K. Chứng minh AK đi qua trung điểm của BC.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
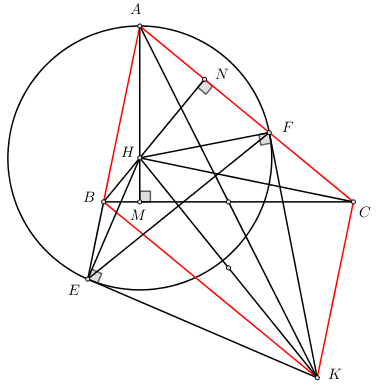
Cho tam giác ABC có ba góc nhọn và \(AB < BC < AC\), kẻ hai đường cao AM và BN cắt nhau tại H \(\left( {M \in BC,\,\,N \in CA} \right)\).
a) Chứng minh tứ giác CMHN nội tiếp.
Xét tứ giác CMHN có: \(\angle CNH = \angle CMH = {90^0} \Rightarrow \angle CNH + \angle CMH = {180^0} \Rightarrow \) Tứ giác CMHN là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Chứng minh \(NA.NC = NH.NB\)
Do tứ giác CMHN là tứ giác nội tiếp (cmt) \( \Rightarrow \angle NHA = \angle NCB\) (góc trong và góc ngoài tại đỉnh đối diện của tứ giác nội tiếp)
Xét tam giác NAH và tam giác NBC có:
\(\begin{array}{l}\angle NHA = \angle NCB\,\,\left( {cmt} \right);\\\angle ANH = \angle BNC = {90^0}\,\,\left( {gt} \right)\end{array}\)
\( \Rightarrow \Delta NAH \sim \Delta NBC\,\,\left( {g.g} \right) \Rightarrow \frac{{NA}}{{NB}} = \frac{{NH}}{{NC}} \Rightarrow NA.NC = NH.NB\)
c) Đường tròn tâm H bán kính HA cắt các tia AB, AC lần lượt tại E, F \(\left( {E \ne A;\,\,F \ne A} \right)\). Chứng minh tứ giác BHFC nội tiếp.
Do \(F \in \left( {H;HA} \right) \Rightarrow HA = HF \Rightarrow \Delta HAF\) cân tại H.
Mà \(HN \bot AF \Rightarrow \) HN là tia phân giác của \(\angle AHF\) (đường cao đồng thời là phân giác).
\( \Rightarrow \angle AHN = \angle FHN\)
Mà \(\angle AHN = \angle BCN\) (do \(\Delta NAH \sim \Delta NBC\))
\( \Rightarrow \angle FHN = \angle BCN\)
Mà \(\angle FHN + \angle FHB = {180^0}\) (kề bù) \( \Rightarrow \angle FHB + \angle BCN = {180^0} \Rightarrow \) Tứ giác BHFC là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800) (đpcm)
\( \Rightarrow \) 4 điểm B, H, F, C cùng thuộc 1 đường tròn (1).
d) Các tiếp tuyến tại E và F của đường tròn \(\left( {H;HA} \right)\) cắt nhau tại K. Chứng minh AK đi qua trung điểm của BC.
Ta có: \(\angle KEH = \angle KFH = {90^0}\,\,\left( {gt} \right) \Rightarrow \angle KEH + \angle KFH = {180^0} \Rightarrow \) Tứ giác KEHF nội tiếp đường tròn đường kính HK.
\( \Rightarrow \) 4 điểm K, E, H, F cùng thuộc 1 đường tròn đường kính HK (2).
Ta có:
\(\Delta HEF\) cân tại H \( \Rightarrow \angle HEF = \angle HFE\).
Mà \(\angle HEF + \angle HFE + \angle EHF = {180^0}\) (tổng ba góc trong tam giác).
\( \Rightarrow \angle HFE = \frac{{{{180}^0} - \angle EHF}}{2} = {90^0} - \frac{1}{2}\angle EHF\)
Lại có \(\angle EHF = 2\angle EAF\) (góc nội tiếp và góc ở tâm cùng chắn cung EF)
\( \Rightarrow \angle HFE = {90^0} - \angle EAF = {90^0} - \angle BAN = \angle ABN\)
Mà \(\angle ABN + \angle EBH = {180^0}\) (kề bù) \( \Rightarrow \angle HFE + \angle EBH = {180^0} \Rightarrow \) Tứ giác BHFE là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
\( \Rightarrow \) 4 điểm B, H, F, E cùng thuộc 1 đường tròn (3)
Từ (1), (2) và (3) \( \Rightarrow \) 6 điểm B, H, F, C, K, E cùng thuộc đường tròn đường kính HK.
\( \Rightarrow \angle HBK = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính HK) \( \Rightarrow BH \bot BK\).
Mà \(BH \bot AC\,\,\left( {gt} \right) \Rightarrow BK//AC\)
Tương tự ta có \(\angle HCK = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính HK) \( \Rightarrow CH \bot CK\).
Mà \(CH \bot AB\) (H là trực tâm của tam giác ABC) \( \Rightarrow AB//CK\)
Xét tứ giác ABKC có: \(\left\{ \begin{array}{l}BK//AC\\AB//CK\end{array} \right. \Rightarrow \)Tứ giác ABKC là hình bình hành (Tứ giác có các cặp cạnh đối song song)
\( \Rightarrow \) Hai đường chéo AK và BC cắt nhau tại trung điểm mỗi đường (Tính chất hình bình hành)
\( \Rightarrow \) AK đi qua trung điểm của BC (đpcm).

