Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường c

Câu hỏi
Nhận biếtCho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao AA’, BB’, CC’ của tam giác ABC cắt nhau tại H. Đường thẳng AO cắt đường tròn tâm O tại D khác A.
a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.
b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
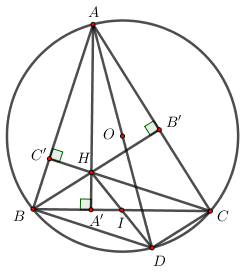
a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.
Xét tứ giác AB’HC’ có \(\angle AB'H + \angle AC'H = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác AB’HC’ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.
Ta có \(\angle ABD = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AB \bot BD\).
Mà \(CH \bot AB\,\,\left( {gt} \right) \Rightarrow BD\parallel CH\)
Chứng minh tương tự ta có \(CD\parallel BH\).
\( \Rightarrow \) Tứ giác BHCD là tứ giác nội tiếp (Tứ giác có các cặp cạnh đối song song)
Mà \(BC \cap HD = I\,\,\left( {gt} \right) \Rightarrow I\) là trung điểm của BC.
c) Tính \(\frac{{AH}}{{AA'}} + \frac{{BH}}{{BB'}} + \frac{{CH}}{{CC'}}\).
Ta có:
\(\frac{{{S_{HBC}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}HA'.BC}}{{\frac{1}{2}AA'.BC}} = \frac{{HA'}}{{AA'}} \Rightarrow 1 - \frac{{{S_{HBC}}}}{{{S_{ABC}}}} = 1 - \frac{{HA'}}{{AA'}} = \frac{{AA' - HA'}}{{AA'}} = \frac{{AH}}{{AA'}}\)
Chứng minh tương tự ta có: \(\frac{{BH}}{{BB'}} = 1 - \frac{{{S_{HAC}}}}{{{S_{ABC}}}};\,\,\frac{{CH}}{{CC'}} = 1 - \frac{{{S_{HAB}}}}{{{S_{ABC}}}}\)
\( \Rightarrow \frac{{AH}}{{AA'}} + \frac{{BH}}{{BB'}} + \frac{{CH}}{{CC'}} = 1 - \frac{{{S_{HBC}}}}{{{S_{ABC}}}} + 1 - \frac{{{S_{HAC}}}}{{{S_{ABC}}}} + 1 - \frac{{{S_{HAB}}}}{{{S_{ABC}}}} = 3 - \frac{{{S_{HBC}} + {S_{HAC}} + {S_{HAB}}}}{{{S_{ABC}}}} = 3 - 1 = 2\).

