Cho đường tròn ( O;R ) đường kính AB và điểm C bất kỳ thuốc đường tròn

Câu hỏi
Nhận biếtCho đường tròn \(\left( {O;R} \right)\) đường kính AB và điểm C bất kỳ thuốc đường tròn (C khác A và B). Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BC ở D. Đường thẳng tiếp xúc với đường tròn tại C cắt AD ở E.
1. Chứng minh bốn điểm A,E,C,O cùng thuộc một đường tròn.
2. Chứng minh \(BC.BD = 4{R^2}\) và OE song song với BD.
3. Đường thẳng kẻ qua O và vuông góc với BC tại N cắt tia EC ở F. Chứng minh BF là tiếp tuyến của đường tròn \(\left( {O;R} \right)\)
4. Gọi H là hình chiếu của C trên AB, M là giao của AC và OE. Chứng minh rằng khi điểm C di động trên đường tròn \(\left( {O;R} \right)\) và thỏa mãn yêu cầu đề bài thì đường tròn ngoại tiếp tam giác HMN luôn đi qua một điểm cố định.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
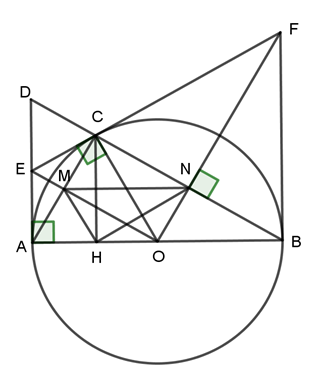
Cho đường tròn \(\left( {O;R} \right)\) đường kính AB và điểm C bất kỳ thuốc đường tròn (C khác A và B). Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BC ở D. Đường thẳng tiếp xúc với đường tròn tại C cắt AD ở E.
1. Chứng minh bốn điểm A, E, C, O cùng thuộc một đường tròn.
AE là tiếp tuyến tại A của \(\left( {O;R} \right) \Rightarrow \angle EAO = {90^o}\)
CE là tiếp tuyến tại C của \(\left( {O;R} \right) \Rightarrow \angle ECO = {90^o}\)
\( \Rightarrow \) C, A cùng thuộc đường tròn đường kính OE
\( \Rightarrow \) A, E, C, O cùng thuộc đường tròn đường kính OE
2. Chứng minh \(BC.BD = 4{R^2}\) và OE song song với BD.
Ta có điểm C thuộc \(\left( O \right)\) đường kính \(AB = 2R\)
\( \Rightarrow \)\(\angle ACB = {90^o} \Rightarrow AC \bot BD\)
\( \Rightarrow \) AC là đường cao trong \(\Delta ABD\)
Xét \(\Delta ABD\) vuông tại A đường cao AC ta có:
\(BC.BD = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\)
Ta có AE là tiếp tuyến tại A của \(\left( {O;R} \right)\)
CE là tiếp tuyến tại C của \(\left( {O;R} \right)\)
\(AE \cap CE = \left\{ E \right\}\)
\( \Rightarrow \) \(OE \bot AC\) (tính chất hai tiếp tuyến cắt nhau)
Mà \(BD \bot AC\) (chứng minh trên) \( \Rightarrow \) \(OE// BD\) (từ vuông góc đến song song)
3. Đường thẳng kẻ qua O và vuông góc với BC tại N cắt tia EC ở F. Chứng minh BF là tiếp tuyến của đường tròn \(\left( {O;R} \right)\)
Ta có \(OF \bot BC\) tại N (gt) \( \Rightarrow \)\(\angle BOF = \angle COF = \frac{1}{2}\angle BOC\) (đường cao đồng thời là đường trung tuyến trong tam giác cân)
Mặt khác \(\angle BCF = \frac{1}{2}\angle BOC\) (CF là tiếp của \(\left( O \right)\) tại C)
\( \Rightarrow \angle BOF = \angle BCF\left( { = \frac{1}{2}\angle BOC} \right)\) \( \Rightarrow \) BOCF là tứ giác nội tiếp
\( \Rightarrow \angle OBF + \angle OCF = {180^o} \Leftrightarrow \angle OBF + {90^o} = {180^o}\) (\(\angle OCF = {90^o}\) do CF là tiếp tuyến của \(\left( O \right)\) tại C)
\( \Rightarrow \angle OBF = {90^o} \Rightarrow BF\) là tiếp tuyến của \(\left( {O;R} \right)\)
4. Gọi H là hình chiếu của C trên AB, M là giao của AC và OE. Chứng minh rằng khi điểm C di động trên đường tròn \(\left( {O;R} \right)\) và thỏa mãn yêu cầu đề bài thì đường tròn ngoại tiếp tam giác HMN luôn đi qua một điểm cố định.
Ta có \(OE\parallel CA\) (chứng minh trên) \( \Rightarrow \angle OMC = {90^o}\)
Mặt khác \(\angle MCN = \angle ONC = {90^o}\) \( \Rightarrow \,OMCN\) là hình chữ nhật \( \Rightarrow \) \(\angle OMN = \angle OCN\) (hai góc nội tiếp cùng chắn cung \(ON\))
Ta có \(\angle OHC = \angle ONC = {90^o}\) \( \Rightarrow \) OHCN là tứ giác nội tiếp \( \Rightarrow \) \(\angle OHN = \angle OCN\) (hai góc nội tiếp cùng chắn cung \(ON\))
\( \Rightarrow \angle OMN = \angle OHN\left( { = \angle OCN} \right)\)
\( \Rightarrow \) HMNO là tứ giác nội tiếp (dhnb)
\( \Rightarrow \) Đường tròn ngoại tiếp tam giác HMN luôn đi qua O là điểm cố định. (đpcm)

