Cho tam giác ABC cân tại A. Gọi I là tâm đường tròn nội tiếp tam giác,
Câu hỏi
Nhận biếtCho tam giác ABC cân tại A. Gọi I là tâm đường tròn nội tiếp tam giác, K là tâm đường tròn bàng tiếp góc A và O là trung điểm của IK.
a) CMR: 4 điểm B, I, C, K cùng thuộc (O).
b) CMR: AC là tiếp tuyến của (O).
c) Tính tổng diện tích các hình viên phân giới hạn bởi các cung nhỏ CI, IB, BK, KC và các dây cung tương ứng của (O) biết AB = 20, BC = 24.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
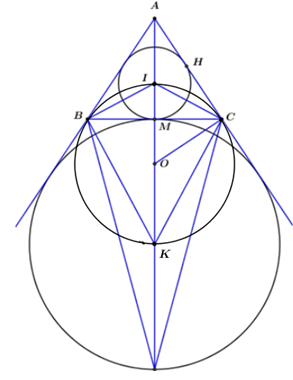
a) CMR: 4 điểm B, I, C, K cùng thuộc (O).
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên IC là phân giác trong của góc C.
Vì K là tâm đường tròn ngoại tiếp tam giác ABC của góc A nên CK là phân giác ngoài của góc C.
Theo tính chất phân giác trong và phân giác ngoài ta có IC vuông CK nên \( \angle ICK={{90}^{0}}\)
Chứng minh hoàn toàn tương tự ta có: \(\angle IBK={{90}^{0}}\)
Xét tứ giác BICK ta có: \( \angle IBK+\angle ICK={{90}^{0}}+{{90}^{0}}={{180}^{0}}.\)
\( \Rightarrow BICK\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng \( {{180}^{0}}\) )
Do O là trung điểm của IK nên theo tính chất trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì OC = OI = OK.
Vậy O là tâm đường tròn ngoại tiếp tứ giác IBKC.
b) CMR: AC là tiếp tuyến của (O).
Ta có : Tam giác IOC cân tại O nên : \( \angle OIC=\angle OCI.\)
Mặt khác, theo tính chất góc ngoài của tam giác ta có :
\( \begin{align} & \angle OIC=\angle IAC+\angle ACI=\frac{1}{2}\angle BAC+\frac{1}{2}\angle ACB=\frac{1}{2}\angle BAC+\frac{1}{2}\angle ABC \\ & \Rightarrow \angle ICO+\angle ICA=\frac{1}{2}\angle BAC+\frac{1}{2}\angle ABC+\frac{1}{2}\angle ACB=\frac{1}{2}{{.180}^{0}}={{90}^{0}} \\ & \Rightarrow OC\bot CA. \\\end{align}\)
Do đó AC là tiếp tuyến của (O) tại C (đpcm).
c) Tính tổng diện tích các hình viên phân giới hạn bởi các cung nhỏ CI, IB, BK, KC và các dây cung tương ứng của (O) biết AB = 20, BC = 24.
Gọi diện tích hình cần tính là S, diện tích hình tròn (O) là S’, gọi giao điểm BC và IK là M.
Ta có ngay :
\( \begin{align} & S=S'-{{S}_{ICKB}}=\pi I{{O}^{2}}-{{S}_{IBK}}-{{S}_{IKC}} \\ & =\pi \frac{I{{K}^{2}}}{4}-\frac{BM.IK}{2}-\frac{CM.IK}{2} \\ & =\pi \frac{I{{K}^{2}}}{4}-\frac{BC.IK}{2}. \\\end{align}\)
Ta có :
\( \begin{align} & \ \ \ \ \ {{S}_{ABC}}=\frac{1}{2}AM.BC=\frac{AB+BC+CA}{2}.IM \\ & \Leftrightarrow \sqrt{A{{B}^{2}}-B{{M}^{2}}}.24=\left( AB+BC+CA \right).IM \\ & \Leftrightarrow \sqrt{{{20}^{2}}-{{\left( \frac{24}{2} \right)}^{2}}}.24=\left( 20.2+24 \right).IM \\ & \Leftrightarrow IM=6. \\\end{align}\)
Áp dụng hệ thức lượng trong tam giác \( IBM\) vuông tại \(B\) có đường cao \( BM\) ta có :
\( \begin{align} & B{{M}^{2}}=IM.MK\Leftrightarrow MK=\frac{B{{M}^{2}}}{IM}=\frac{{{12}^{2}}}{6}=24. \\ & \Rightarrow IM=IM+MK=6+24=30. \\ & \Rightarrow S=\frac{1}{4}\pi I{{K}^{2}}-\frac{1}{2}BC.IK=\frac{1}{4}\pi {{.30}^{2}}-\frac{1}{2}.24.30 \\ & \ \ \ \ \ \ \ =225\pi -360\approx 346,86\ \ \left( dvdt \right). \\\end{align}\)
bài rất bổ ích cho tôi chỉ có mấy phần chưa hiểu , cảm ơn rất nhiều vì đã giải bài này