Cho đường tròn (O) đường kính AB và một dây CD vuông góc với AB tại H

Câu hỏi
Nhận biếtCho đường tròn (O) đường kính AB và một dây CD vuông góc với AB tại H (H không trừng với các điểm A, B, O). Gọi M là trung điểm của AD. Chứng minh:
a) Bốn điểm O, M, D, H cùng thuộc một đường tròn.
b) MH vuông góc với BC.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
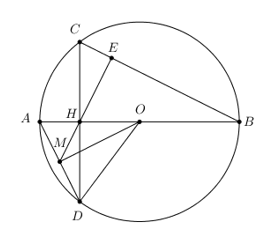
a) Bốn điểm O, M, D, H cùng thuộc một đường tròn.
Vì M là trung điểm của AD \( \Rightarrow OM \bot AD\) (quan hệ vuông góc giữa đường kính và dây cung)
\( \Rightarrow \) Điểm M, H cùng nhìn OD dưới một góc 900.
\( \Rightarrow \) Tứ giác OHMD là tứ giác nội tiếp (Tứ giác có hai đỉnh cùng nhìn một cạnh dưới các góc bằng nhau).
Vậy bốn điểm O, M, D, H cùng thuộc một đường tròn.
b) MH vuông góc với BC.
Kéo dài MH cắt BC tại E.
Xét tam giác vuông ADH có HM là đường trung tuyến ứng với cạnh huyền AD \( \Rightarrow HM = \frac{1}{2}AD = MD \Rightarrow \Delta MHD\) cân tại M \( \Rightarrow \widehat {MHD} = \widehat {MDH} = \widehat {ADC}\)
Lại có \(\widehat {ADC} = \widehat {ABC}\) (hai góc nội tiếp cùng chắn cung AC).
\(\widehat {MHD} = \widehat {CHE}\) (đối đỉnh)
\( \Rightarrow \widehat {CHE} = \widehat {ABC}\).
Xét tam giác vuông BCH có \(\widehat {ABC} + \widehat {HCB} = {90^0} \Rightarrow \widehat {CHE} + \widehat {HCB} = {90^0} \Rightarrow \Delta CHE\) vuông tại E.
\( \Rightarrow HE \bot BC\).
Vậy \(MH \bot BC\).

