Cho cot alpha = - căn 3 ,,( 3pi over 2 < alpha < 2pi ). Khi đó sthuộc alpha = ?

Câu hỏi
Nhận biếtCho \(\cot \alpha = - \sqrt 3 ,\,\,\left( {{{3\pi } \over 2} < \alpha < 2\pi } \right)\). Khi đó \(\sin \alpha = ?\)
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
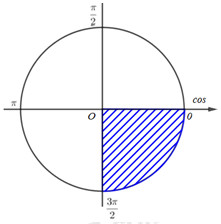
Ta có:
\(1 + {\cot ^2}\alpha = {1 \over {{{\sin }^2}\alpha }} \Leftrightarrow 1 + {\left( { - \sqrt 3 } \right)^2} = {1 \over {{{\sin }^2}\alpha }} \Leftrightarrow {\sin ^2}\alpha = {1 \over 4} \Leftrightarrow \left[ \matrix{ \sin \alpha = {1 \over 2} \hfill \cr \sin \alpha = - {1 \over 2} \hfill \cr} \right.\)
Vì \({{3\pi } \over 2} < \alpha < 2\pi \Rightarrow \sin \alpha < 0 \Rightarrow \sin \alpha = - {1 \over 2}\)
Chọn: D.
