Cho phương trình x2 – 4x + 2m – 3 = 0, (1) với m là tham số. Tìm các
Câu hỏi
Nhận biếtCho phương trình x2 – 4x + 2m – 3 = 0, (1) với m là tham số. Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt x1, x2 thỏa mãn: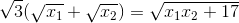
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Chú ý: Vì x1, x2 nằm trong các căn bậc hai nên phải có điều kiện x1 ≥ 0, x2 ≥ 0.
+) Phương trình có hai nghiệm phân biệt x1, x2 ≥ 0
<=> (1) ∆' > 0 <=> 4 - 2m + 3 > 0
(2) S > 0 <=> 4 > 0 (luôn đúng)
(3) P ≥ 0 <=> 2m - 3 ≥ 0
=> 
≤ m < 
+) Với ≤ m < phương trình (1) có hai nghiệm phân biệt x1, x2 ≥ 0
Áp dụng định lý Vi-et ta có: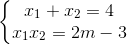 
+) Ta có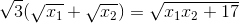 
<=> 
<=> 
<=> 
<=> 
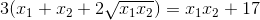
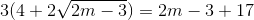
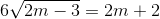
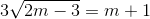<=> Đồng thời hai điều kiện:
(1) m ≥ -1
(2)
9(2m – 3) = m2 + 2m + 1 <=> m2 – 16m + 28 = 0 <=> m = 2 và m = 14
So sánh với các điều kiện ta có giá trị m thỏa mãn là m = 2.
