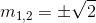Giả sử đường thẳng (d) cắt parabol (P) tại A(x1, y1) và B(x2, y2). Tìm
Câu hỏi
Nhận biếtGiả sử đường thẳng (d) cắt parabol (P) tại A(x1, y1) và B(x2, y2). Tìm giá trị của m để 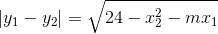
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
x1, x2 là hai nghiệm của phương trình x2 – mx – 2 = 0. Theo Vi-et ta có:
x1 + x2 = m và x1x2 = -2
Tọa độ giao điểm của (d) và (P) là nghiệm của hệ phương trình: 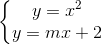
Vậy 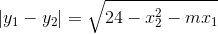
<=> 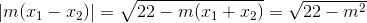 (*)
(*)
ĐK: m2 ≤ 22 (*) <=> m2 (x1 – x2)2 = 22 – m2
<=> m2[(x1 + x2)2 – 4x1x2] = 22 – m2
<=> m2 (m2 + 8) = 22 – m2
<=> m4 + 9m2 – 22 = 0
Đặt m2 = t (đk: 0 ≤ t ≤ 22). Phương trình trở thành t2 + 9t – 22 = 0
=> t1 = -11 (không thỏa mãn đk); t2 = 2 (thỏa mãn)
=>