Cho hình chữ nhật ABCD có AB = acăn 2 ,AD = a. Gọi M là điểm nằm t

Câu hỏi
Nhận biếtCho hình chữ nhật \(ABCD \) có \(AB = a \sqrt 2 ,AD = a. \) Gọi \(M \) là điểm nằm trên cạnh \(AB \) sao cho \(AM = a. \) Tính \( \overrightarrow {MD} . \overrightarrow {AC} . \)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
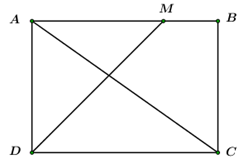
Áp dụng định lý Pitago ta có:
\(\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {a^2}} = a\sqrt 3 .\\\overrightarrow {MD} .\overrightarrow {AC} = \left( {\overrightarrow {MA} + \overrightarrow {AD} } \right)\overrightarrow {AC} = \overrightarrow {MA} .\overrightarrow {AC} + \overrightarrow {AD} .\overrightarrow {AC} \\ = MA.AC.\cos \left( {\overrightarrow {MA} ,\,\,\overrightarrow {AC} } \right) + AD.AC.\cos \left( {\overrightarrow {AD} ,\,\,\overrightarrow {AC} } \right)\\ = a.a\sqrt 3 .\cos \left( {180^\circ - \angle MAC} \right) + a.a\sqrt 3 .\cos \angle CAD\\ = {a^2}\sqrt 3 .\left( { - \cos \angle MAC} \right) + {a^2}\sqrt 3 \cos \angle CAD\\ = a.a\sqrt 3 .\left( { - \frac{{\sqrt 2 }}{{\sqrt 3 }}} \right) + a.a\sqrt 3 .\frac{1}{{\sqrt 3 }} = \left( {1 - \sqrt 2 } \right){a^2}.\end{array}\)
Chọn A.
