1) Lập bảng biến thiên và vẽ đồ thị hàm số y = x^2 - 4x + 3 2) Giải p

Câu hỏi
Nhận biết1) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} - 4x + 3 \)
2) Giải phương trình \( \sqrt {2{x^2} + 4x - 1} = x + 1 \)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
1) +) TXĐ: \(D = R\)
+) Đỉnh \(I\left( {2; - 1} \right)\), trục đối xứng \(x = 2\)
+) Hàm số đồng biến trên \(\left( {2; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;2} \right)\).
BBT:
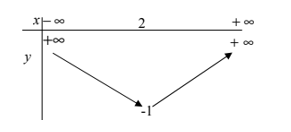
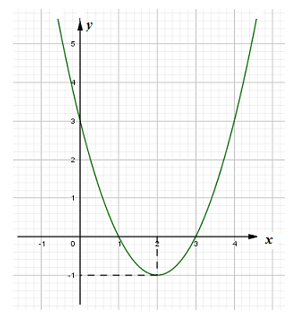
+) Đồ thị:
Giao với Ox: \(y = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
Giao với Oy: \(x = 0 \Leftrightarrow y = 3\)
b) \(\sqrt {2{x^2} + 4x - 1} = x + 1 \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\2{x^2} + 4x - 1 = {\left( {x + 1} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\2{x^2} + 4x - 1 = {x^2} + 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\{x^2} + 2x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\\left[ \begin{array}{l}x = - 1 + \sqrt 3 \,\,\left( {tm} \right)\\x = - 1 - \sqrt 3 \,\,\left( {ktm} \right)\end{array} \right.\end{array} \right. \Leftrightarrow x = - 1 + \sqrt 3 \)
Vậy nghiệm của phương trình là \(x = - 1 + \sqrt 3 \).
