a) Vẽ đồ thị ( P ) của hàm số y = 2x^2 trên hệ trục tọa độ Oxy. b) Tì

Câu hỏi
Nhận biếta) Vẽ đồ thị \( \left( P \right) \) của hàm số \(y = 2{x^2} \) trên hệ trục tọa độ \(Oxy. \)
b) Tìm các giá trị của tham số \(m \) để đường thẳng \( \left( {{d_m}} \right): \; \;y = \left( {{m^2} + m - 4} \right)x + m - 7 \) song song với đường thẳng \( \left( d \right): \; \;y = 2x - 5. \)
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
a) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = 2{x^2}\) trên hệ trục tọa độ \(Oxy.\)
+) Vẽ đồ thị hàm số \(\left( P \right):\)
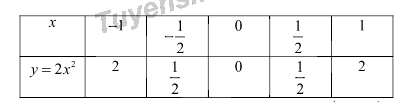
Đồ thị \(\left( P \right)\) là parabol đi qua các điểm \(\left( { - 1;\;2} \right),\;\;\left( { - \frac{1}{2};\;\frac{1}{2}} \right),\;\left( {0;\;0} \right),\;\left( {\frac{1}{2};\;\frac{1}{2}} \right),\;\;\left( {1;\;2} \right).\)
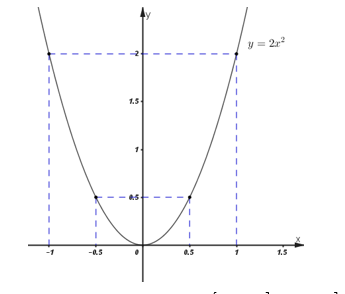
b) Tìm các giá trị của tham số \(m\) để đường thẳng \(\left( {{d_m}} \right):\;\;y = \left( {{m^2} + m - 4} \right)x + m - 7\) song song với đường thẳng \(\left( d \right):\;\;y = 2x - 5.\)
Đường thẳng \(\left( {{d_m}} \right)//d \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 4 = 2\\m - 7 \ne - 5\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 6 = 0\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 2} \right)\left( {m + 3} \right) = 0\\m \ne 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m - 2 = 0\\m + 3 = 0\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 3\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow m = - 3.\end{array}\)
Vậy \(m = - 3\)

