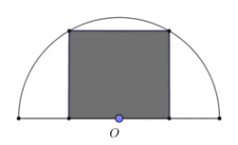
Từ một miếng tôn có hình dạng là nửa hình tròn bán kính 1m, người ta c
Câu hỏi
Nhận biếtTừ một miếng tôn có hình dạng là nửa hình tròn bán kính 1m, người ta cắt ra một hình chữ nhật (phần tô đậm như hình vẽ). Phần hình chữ nhật có diện tích lớn nhất có thể cắt được là:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
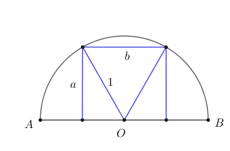
Gọi kích thước của miếng tôn như hình vẽ.
Áp dụng định lý Pi-ta-go ta có:
\({a^2} + {\left( {\frac{b}{2}} \right)^2} = 1 \Leftrightarrow {a^2} = \frac{{4 - {b^2}}}{4} \Leftrightarrow a = \frac{{\sqrt {4 - {b^2}} }}{2}.\)
Khi đó diện tích miếng tôn hình chữ nhật là:
\(S = ab = \frac{{b\sqrt {4 - {b^2}} }}{2}.\)
Áp dụng bất đẳng thức Cô-si cho hai số ta có: \({b^2} + \sqrt {{{\left( {4 - {b^2}} \right)}^2}} \ge 2b\sqrt {4 - {b^2}} \Leftrightarrow b\sqrt {4 - {b^2}} \le \frac{{{b^2} + 4 - {b^2}}}{2} = 2.\)
\( \Rightarrow S = \frac{{b\sqrt {4 - {b^2}} }}{2} \le \frac{2}{2} = 1.\)
Dấu “=” xảy ra \( \Leftrightarrow b = \sqrt {4 - {b^2}} \Leftrightarrow {b^2} = 4 - {b^2} \Leftrightarrow {b^2} = 2 \Leftrightarrow b = \sqrt 2 .\)
Vậy diện tích lớn nhất có thể là \(1{m^2}.\)
Chọn C.


