Cho cos alpha = 5 over 13,,,( 3pi over 2 < alpha < 2pi ). Khi đó t

Câu hỏi
Nhận biếtCho \( \cos \alpha = {5 \over {13}}, \, \, \left( {{{3 \pi } \over 2} < \alpha < 2 \pi } \right) \). Khi đó \( \tan \alpha = ? \)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
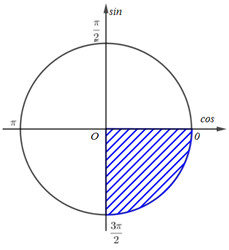
Cách 1:
Ta có:
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\sin ^2}\alpha + {\left( {{5 \over {13}}} \right)^2} = 1 \Leftrightarrow {\sin ^2}\alpha = {{144} \over {169}} \Leftrightarrow \left[ \matrix{ \sin \alpha = {{12} \over {13}} \hfill \cr \sin \alpha = - {{12} \over {13}} \hfill \cr} \right.\)
Vì \({{3\pi } \over 2} < \alpha < 2\pi \Rightarrow \sin \alpha < 0 \Rightarrow \sin \alpha = - {{12} \over {13}} \Rightarrow \,\tan \alpha = {{\sin \alpha } \over {\cos \alpha }} = {{ - {{12} \over {13}}} \over {{5 \over {13}}}} = - {{12} \over 5}\)
Cách 2:
Ta có:
\(1 + {\tan ^2}\alpha = {1 \over {{{\cos }^2}\alpha }} \Leftrightarrow 1 + {\tan ^2}\alpha = {1 \over {{{\left( {{5 \over {13}}} \right)}^2}}} \Leftrightarrow 1 + {\tan ^2}\alpha = {{169} \over {25}} \Leftrightarrow {\tan ^2}\alpha = {{144} \over {25}} \Leftrightarrow \left[ \matrix{ \tan \alpha = {{12} \over 5} \hfill \cr \tan \alpha = - {{12} \over 5} \hfill \cr} \right.\)
Vì \({{3\pi } \over 2} < \alpha < 2\pi \Rightarrow \left\{ \matrix{ \sin \alpha < 0 \hfill \cr \cos \alpha > 0 \hfill \cr} \right. \Rightarrow \tan \alpha < 0 \Rightarrow \,\tan \alpha = - {{12} \over 5}\)
Chọn: A.
