Cho đường tròn tâm (O,R). A là điểm trên đường tròn, dựng đường tròn

Câu hỏi
Nhận biếtCho đường tròn tâm (O,R). A là điểm trên đường tròn, dựng đường tròn tâm O’ đường kính OA. Gọi M là điểm nằm trên (O’), tia OM cắt đường tròn (O, R) tại N. Khi đó, kết luận nào sau đây đúng?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
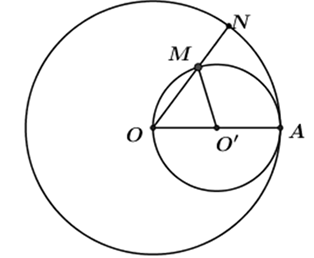
Hai đường tròn (O) và (O’) tiếp xúc nhau tại A.
Tam giác O’OM có \(OO=OM\), suy ra tam giác O’OM cân, \(O'A=\frac{1}{2}R\)
Đặt \(\widehat{AOM}={{n}^{0}}\) thì \(\widehat{A{O}'M}=2{{n}^{0}}\) (mối quan hệ giữa góc nội tiếp và góc ở
Tâm cùng chắn 1 cung).
Suy ra số đo cung AM là \(2{{n}^{0}}.\)
Xét (O’) có độ dài cung AM là: \(\frac{\pi .\frac{R}{2}.2n}{180}=\frac{\pi .Rn}{180}\)
Xét (O) có độ dài cung AN là: \(\frac{\pi .Rn}{180}\)
Vậy \(\overset\frown{AM}=\overset\frown{AN}\)
Chọn A

