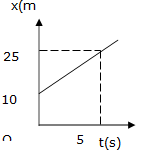Một thanh cứng, mảnh AB có chiều dài l = 2m dựng đứng sát bức tường th
Câu hỏi
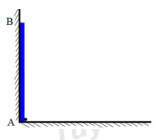
Nhận biếtMột thanh cứng, mảnh AB có chiều dài \(l = 2m\) dựng đứng sát bức tường thẳng đứng như hình.

Ở đầu A của thanh có một con kiến. Khi đầu A của thanh bắt đầu chuyển động trên sàn ngang về bên phải theo phương vuông góc với bức tường thì con kiến cũng bắt đầu bò dọc theo thanh. Đầu A chuyển động thẳng đều với vận tốc \({v_1} = 0,5cm/s\) so với sàn kể từ vị trí tiếp xúc với bức tường. Con kiến bò thẳng đều với vận tốc \({v_2} = 0,2cm/s\) so với thanh kể từ đầu A. Độ cao cực đại của con kiến đối với sàn ngang là bao nhiêu? Biết rằng đầu B của thanh luôn tiếp xúc vưới tường.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Hướng dẫn giải:
Ta có:
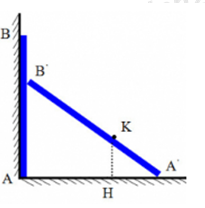
+ Khi đầu A của thanh di chuyển từ A đến A’ thì con kiến di chuyển từ A’ đến K trong cùng một khoảng thời gian.
+ Khi đó: \(\frac{{{s_{{\rm{AA'}}}}}}{{{v_1}}} = \frac{{{s_{A'K}}}}{{{v_2}}} \to \frac{{{s_{{\rm{AA'}}}}}}{{{s_{A'K}}}} = \frac{{{v_1}}}{{{v_2}}} = \frac{{0,5}}{{0,2}} = 2,5\)
=> Nếu quãng đường con kiến di chuyển là \({s_{A'K}} = x \to {s_{AA'}} = 2,5x\)
Từ hình, ta có:
\({\left( {AB'} \right)^2} = {2^2} - {\left( {2,5{\rm{x}}} \right)^2} = 4 - 6,25{{\rm{x}}^2}\)
Mặt khác, ta có:
\(\begin{array}{*{20}{l}}{\Delta A'KH\~\Delta A'B'A}\\{ \to \frac{{HK}}{{AB'}} = \frac{{A'K}}{{A'B'}}}\\{ \to H{K^2} = {{\left( {AB'} \right)}^2}{{\left( {\frac{{A'K}}{{A'B'}}} \right)}^2} = (4 - 6,25{{\rm{x}}^2})\frac{{{x^2}}}{4} = - 1,5625{{\rm{x}}^4} + {x^2}}\end{array}\)
Để HKcó giá trị cực đại thì: \({x^2} = - \frac{b}{{2{\rm{a}}}} = \frac{1}{{2.1,5625}} = 0,32\)
Khi đó: \(H{K_{{\rm{max}}}} = \sqrt { - 1,5625.0,{{32}^2} + 0,32} = 0,4(m)\)
Chọn A
Luyện tập
Câu hỏi liên quan
-

Trên hình là đồ thị tọa độ-thời gian của một vật chuyển động
thẳng.
Cho biết kết luận nào sau đây là sai?

Một xe chuyển động thẳng không đổi chiều; 2 giờ đầu xe chạy với vận tốc trung bình 60km/h, 3 giờ sau xe chạy với vận tốc trung bình 40km/h. Vận tốc trung bình của xe trong suốt thời gian chạy là:

Một vật chuyển động thẳng không đổi chiều. Trên quãng đường AB, vật đi nửa quãng đường đầu với vận tốc v1 = 20m/s, nửa quãng đường sau vật đi với vận tốc v2 = 5m/s. Vận tốc trung bình trên cả quãng đường là:

Phương trình chuyển động của một chất điểm dọc theo trục Ox có dạng : x = 5 + 60t (x : m, t đo bằng giờ).Chất điểm đó xuất phát từ điểm nào và chuyển động với vận tốc bằng bao nhiêu ?


Một xe chuyển động thẳng không đổi chiều có vận tốc trung bình là 20Km/h trên 1/4 đoạn đường đầu và 40Km/h trên 3/4 đoạn đường còn lại. Vận tốc trung bình của xe trên cả đoạn đường là :

Một ngừơi đi xe đạp trên 2/3 đoạn đừơng đầu với vận tốc trung bình 10km/h và 1/3 đoạn đừơng sau với vận tốc trung bình 20km/h. Vận tốc trung bình của ngừơi đi xe đạp trên cả quảng đừơng là

Phương trình của một vật chuyển động thẳng có dạng: x = -3t + 4 (m; s). Kết luận nào sau đây đúng

Một vật chuyển động thẳng không đổi chiều trên 1 quãng đường dài 40m. Nửa quãng đường đầu vật đi hết thời gian t1 = 5s, nửa quãng đường sau vật đi hết thời gian t2 = 2s. Tốc độ trung bình trên cả quãng đường là:

Một vật chuyển động thẳng đều với vận tốc v = 2 m/ s. Và lúc t = 2 s thì vật có toạ độ x = 5 m. Phương trình toạ độ của vật là