Gọi I là tâm đường tròn ngoại tiếp tam giác FDM. Chứng minh ba điểm D
Câu hỏi
Nhận biếtGọi I là tâm đường tròn ngoại tiếp tam giác FDM. Chứng minh ba điểm D, I, B thẳng hàng, từ đó suy ra góc ABI có số đo không đổi khi M di chuyển trên cung BD.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Gọi H là trung điểm của DF. Suy ra IH ┴ DF và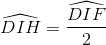 
(3)
Trong đường tròn (I) ta có: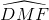 
và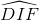 
lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung DF. Suy ra 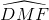(4)
Từ (3) và (4) suy ra 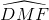hay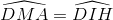 
Trong đường tròn (O) ta có: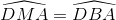 
(góc nội tiếp cùng chắn cung DA)
=> 
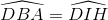
Vì IH và BC cùng vuông góc với EC nên suy ra IH // BC. Do đó,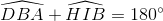 
=> 
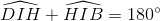
=> Ba điểm D, I, B thẳng hàng.
=> 
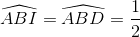sđ cung AD. Vì C cố định nên D cố định
=> 
sđ cung AD không đổi.
Do đó góc ABI có số đo không đổi khi M thay đổi trên cung BD.
