Một viên gạch hình vuông cạnh a,,( cm ) có hoa văn như hình vẽ. M, N,
Câu hỏi
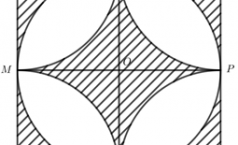
Nhận biếtMột viên gạch hình vuông cạnh \(a\,\,\left( {cm} \right)\) có hoa văn như hình vẽ. M, N, P, Q lần lượt là trung điểm các cạnh AD, AB, BC, CD. Tìm độ dài \(a\) biết diện tích phần gạch chéo là \(200\left( {4 - \pi } \right)\) (cm2)

Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:

Nhận thấy rằng phần gạch trắng tạo bởi 8 hình viên phân bằng nhau.
Gọi \(R = \frac{a}{2}\) là bán kính hình tròn. Diện tích một hình viên phân là:
\(S = \frac{{\pi {R^2}}}{4} - \frac{{{R^2}}}{2} = \frac{{{R^2}}}{4}\left( {\pi - 2} \right) = \frac{{{a^2}}}{{16}}\left( {\pi - 2} \right)\,\,\,\left( {c{m^2}} \right)\)
Vậy diện tích hình gồm 8 viên phân bằng \(\frac{{{a^2}}}{2}\left( {\pi - 2} \right)\,\,\left( {c{m^2}} \right)\)
Diện tích phần gạch chéo bằng: \({a^2} - \frac{{{a^2}\left( {\pi - 2} \right)}}{2} = \frac{{{a^2}\left( {4 - \pi } \right)}}{2}\,\,\,\left( {c{m^2}} \right)\)
Vì diện tích phần gạch chéo là \(200\left( {4 - \pi } \right)\,\,\,\left( {c{m^2}} \right)\) nên ta có:
\(\frac{{{a^2}\left( {4 - \pi } \right)}}{2} = 200\left( {4 - \pi } \right) \Leftrightarrow {a^2} = 400 \Leftrightarrow a = 20\,\,\,\left( {cm} \right)\)
Vậy \(a = 20\,\,\left( {cm} \right).\)
Chọn B.


