Cho hình thang ABCD với hai cạnh đáy là AB = 2a và CD = 6a. Khi đó giá

Câu hỏi
Nhận biếtCho hình thang ABCD với hai cạnh đáy là AB = 2a và CD = 6a. Khi đó giá trị \( \left| { \overrightarrow {AB} + \overrightarrow {CD} } \right| \) bằng bao nhiêu?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
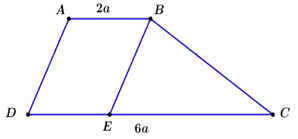
Hình thang ABCD có hai đáy là AB và CD nên \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \)
là hai vectơ cùng phương ngược chiều.
Trên đoạn thẳng DC lấy điểm E sao cho \(DE = AB = 2a.\)
Khi đó ta có: \(\overrightarrow {AB} = \overrightarrow {DE} = \frac{1}{3}\overrightarrow {DC} .\)
\(\begin{array}{l} \Rightarrow \overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {DE} + \overrightarrow {CD} = \frac{1}{3}\overrightarrow {DC} + \overrightarrow {CD} = - \frac{1}{3}\overrightarrow {CD} + \overrightarrow {CD} = \frac{2}{3}\overrightarrow {CD} \\ \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {CD} } \right| = \left| {\frac{2}{3}\overrightarrow {CD} } \right| = \frac{2}{3}.\left| {\overrightarrow {CD} } \right| = \frac{2}{3}.6a = 4a.\end{array}\)
Chọn B.
