Cho hình vuông ABCD cạnh bằng a. Gọi E là trung điểm của CD. Tính độ d

Câu hỏi
Nhận biếtCho hình vuông ABCD cạnh bằng a. Gọi E là trung điểm của CD. Tính độ dài dây cung chung CF của đường tròn đường kính BE và đường tròn đường kính CD.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
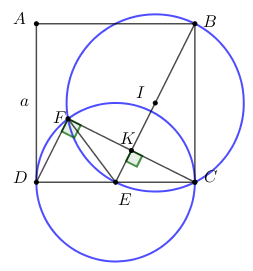
Đặt \(BI = R,\;\;CE = r,\;\;KC = x\;\;\left( {0 < x < a} \right).\)
\(\begin{array}{l}BE = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \sqrt {\frac{{5{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2} \Rightarrow BI = IE = \frac{{a\sqrt 5 }}{4} = R.\\CE = \frac{a}{2} = r,\;\;KE = \sqrt {C{E^2} - K{C^2}} = \sqrt {{r^2} - {x^2}} .\\KI = \sqrt {I{C^2} - K{C^2}} = \sqrt {{R^2} - {x^2}} .\\ \Rightarrow IE = KE + KI\\ \Leftrightarrow R = \sqrt {{R^2} - {x^2}} + \sqrt {{r^2} - {x^2}} \\ \Leftrightarrow {R^2} = {R^2} + {r^2} - 2{x^2} + 2\sqrt {\left( {{R^2} - {x^2}} \right)\left( {{r^2} - {x^2}} \right)} \\ \Leftrightarrow 2{x^2} - {r^2} = 2\sqrt {{R^2}{r^2} - \left( {{R^2} + {r^2}} \right){x^2} + {x^4}} \\ \Leftrightarrow 4{x^4} - 4{r^2}{x^2} + {r^4} = 4{R^2}{r^2} - 4\left( {{R^2} + {r^2}} \right){x^2} + 4{x^4}\;\;\;\left( {2{x^2} \ge {r^2}} \right)\\ \Leftrightarrow 4\left( {{R^2} + {r^2}} \right){x^2} - 4{r^2}{x^2} = 4{R^2}{r^2} - {r^4}\\ \Leftrightarrow 4{R^2}{x^2} = 4{R^2}{r^2} - {r^4}\\ \Leftrightarrow {x^2} = \frac{{4{R^2}{r^2} - {r^4}}}{{4{R^2}}} = \frac{{4.\frac{{5{a^2}}}{{16}}.\frac{{{a^2}}}{4} - \frac{{{a^4}}}{{16}}}}{{4.\frac{{5{a^2}}}{{16}}}} = \frac{{{a^2}}}{5}\\ \Rightarrow KC = x = \frac{{a\sqrt 5 }}{5} \Rightarrow FC = 2x = \frac{{2a\sqrt 5 }}{5}.\end{array}\)
Chọn B

