Gọi H là giao điểm của AB và MO . Chứng minh tứ giác CHOD nội tiếp đườ
Câu hỏi
Nhận biếtGọi H là giao điểm của AB và MO . Chứng minh tứ giác CHOD nội tiếp đường tròn. Suy ra AB là đường phân giác của góc CHD
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
∆ MAO vuông tại A và có AH là đường cao.
=> MA2 = MH.MO
Mà theo câu a, MA2 = MC.MD
Do đó MH.MO = MC.MD; ∆ MHC ~ ∆ MDO (c.g.c)
=> 
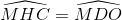
=> Tứ giác CHOD nội tiếp. ( Dấu hiệu nhận biết tứ giác nội tiếp).
Ta có: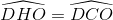 
( vì tứ giác CHDO nội tiếp )
∆ OCD có OC = OD (= R)
=> ∆ OCD cân tại O => 
Mà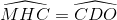 
(chứng minh trên)
Do đó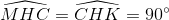 
, 
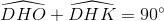
Vậy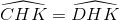 
=> AB là đường phân giác của góc CDH
