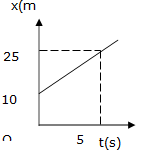Với giá trị nào của m thì hệ phương trình matrixx - y + 1 = 0 hfill

Câu hỏi
Nhận biếtVới giá trị nào của m thì hệ phương trình \( \left \{ \matrix{x - y + 1 = 0 \hfill \cr 2m{x^2} - 2my + 4x + 2m - 3 = 0 \hfill \cr} \right. \) có ít nhất 1 nghiệm:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
\(\eqalign{& \,\,\,\,\,\,\,\,\left\{ \matrix{x - y + 1 = 0 \hfill \cr 2m{x^2} - 2my + 4x + 2m - 3 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{y = x + 1 \hfill \cr 2m{x^2} - 2m\left( {x + 1} \right) + 4x + 2m - 3 = 0 \hfill \cr} \right. \cr & \Leftrightarrow \left\{ \matrix{y = x + 1 \hfill \cr 2m{x^2} - 2mx - 2m + 4x + 2m - 3 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{y = x + 1 \hfill \cr 2m{x^2} - 2\left( {m - 2} \right)x - 3 = 0 \hfill \cr} \right. \cr} \)
Xét phương trình\(2m{x^2} - 2\left( {m - 2} \right)x - 3 = 0\)(1)
Nếu m = 0 thì\((1) \Leftrightarrow 4x - 3 = 0 \Leftrightarrow x = {3 \over 4} \Leftrightarrow y = {7 \over 4}\) (thỏa mãn hệ có ít nhất 1 nghiệm)
Nếu\(m \ne 0\) thì (1) là phương trình bậc hai ẩn x tham số m.
Để hệ đã cho có ít nhất 1 nghiệm thì phương trình (1) có ít nhất 1 nghiệmPhương trình (1) có ít nhất 1 nghiệm \( \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow {\left( {m - 2} \right)^2} + 6m \ge 0\)
\( \Leftrightarrow {m^2} - 4m + 4 + 6m \ge 0\)
\( \Leftrightarrow {m^2} + 2m + 4 \ge 0\)
\( \Leftrightarrow {\left( {m + 1} \right)^2} + 3 \ge 0\) (đúng \(\forall m \in R\)
Vậy với mọi giá trị của thì hệ phương trình đã cho luôn có nghiệm hay có ít nhất 1 nghiệm.
Luyện tập
Câu hỏi liên quan
-

Một vật chuyển động thẳng không đổi chiều. Trên quãng đường AB, vật đi nửa quãng đường đầu với vận tốc v1 = 20m/s, nửa quãng đường sau vật đi với vận tốc v2 = 5m/s. Vận tốc trung bình trên cả quãng đường là:


Một ngừơi đi xe đạp trên 2/3 đoạn đừơng đầu với vận tốc trung bình 10km/h và 1/3 đoạn đừơng sau với vận tốc trung bình 20km/h. Vận tốc trung bình của ngừơi đi xe đạp trên cả quảng đừơng là

Phương trình chuyển động của một chất điểm dọc theo trục Ox có dạng : x = 5 + 60t (x : m, t đo bằng giờ).Chất điểm đó xuất phát từ điểm nào và chuyển động với vận tốc bằng bao nhiêu ?

Trên hình là đồ thị tọa độ-thời gian của một vật chuyển động
thẳng.
Cho biết kết luận nào sau đây là sai?

Một vật chuyển động thẳng không đổi chiều trên 1 quãng đường dài 40m. Nửa quãng đường đầu vật đi hết thời gian t1 = 5s, nửa quãng đường sau vật đi hết thời gian t2 = 2s. Tốc độ trung bình trên cả quãng đường là:

Phương trình của một vật chuyển động thẳng có dạng: x = -3t + 4 (m; s). Kết luận nào sau đây đúng

Một vật chuyển động thẳng đều với vận tốc v = 2 m/ s. Và lúc t = 2 s thì vật có toạ độ x = 5 m. Phương trình toạ độ của vật là

Một xe chuyển động thẳng không đổi chiều; 2 giờ đầu xe chạy với vận tốc trung bình 60km/h, 3 giờ sau xe chạy với vận tốc trung bình 40km/h. Vận tốc trung bình của xe trong suốt thời gian chạy là:

Một xe chuyển động thẳng không đổi chiều có vận tốc trung bình là 20Km/h trên 1/4 đoạn đường đầu và 40Km/h trên 3/4 đoạn đường còn lại. Vận tốc trung bình của xe trên cả đoạn đường là :