Cho a, b, c là ba số dương thỏa mãn điều kiện ab + bc + ca = 1. Tìm gi
Câu hỏi
Nhận biếtCho a, b, c là ba số dương thỏa mãn điều kiện ab + bc + ca = 1. Tìm giá trị nhỏ nhất của biểu thức : P = 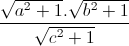 +
+ 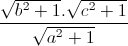 +
+ 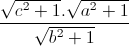
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Vì ab + bc + ca = 1
Ta có a2 + 1 = a2 + ab + bc + ca = a(a + b ) + c(a + b)
Tương tự có b2 + 1 = (a + b)(b + c); c2 + 1 = (a + c)(b + c)
Do đó
P = 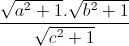 +
+ 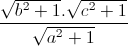 +
+ 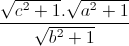
=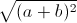 +
+ 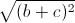 +
+ 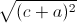
= a + b + b + c + c + a
= 2(a + b + c) = 2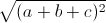
= 2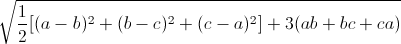
= 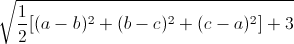 ≥ 2√3
≥ 2√3
Dấu “=” xảy ra khi và chỉ khi a = b = c = 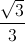
Vậy giá trị nhỏ nhất của biểu thức P là 2√3.


