a) Lập bảng biến thiên và vẽ đồ thị hàm số y = - x^2 - 2x + 3 b) Tìm m để phương trình: x^2 - 2mx

Câu hỏi
Nhận biếta) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = - {x^2} - 2x + 3\)
b) Tìm m để phương trình: \({x^2} - 2mx + {m^2} - 2m + 1 = 0\) có hai nghiệm \({x_1};{x_2}\) sao cho biểu thức \(T = {x_1}{x_2} + 4\left( {{x_1} + {x_2}} \right)\) nhỏ nhất.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
a) + Tập xác định \(D = R\).
+ Bảng biến thiên:
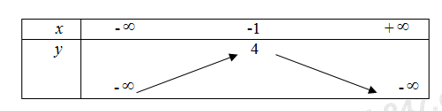
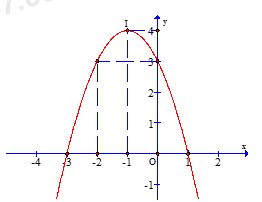
+ Vẽ đồ thị hàm số
+ Đỉnh \(I\left( { - 1;4} \right)\)
+ Trục đối xứng \(x = - 1\)
+ Giao với trục tung \(A\left( {0;3} \right)\)
+ Giao với trục hoành tại \(B\left( {1;0} \right);\,\,B'\left( { - 3;0} \right)\).
Để phương trình có nghiệm thì: \(\Delta ' \ge 0 \Leftrightarrow 2m - 1 \ge 0 \Leftrightarrow m \ge \dfrac{1}{2}\)
b) Ta có: \(\Delta ' = {m^2} - {m^2} + 2m - 1 = 2m - 1\).
Để phương trình có 2 nghiệm \( \Leftrightarrow 2m - 1 \ge 0 \Leftrightarrow m \ge \dfrac{1}{2}\).
Với \(m \ge \dfrac{1}{2}\) theo định lí Viét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = {m^2} - 2m + 1\end{array} \right.\).
\(T = {x_1}{x_2} + 4\left( {{x_1} + {x_2}} \right) = {m^2} - 2m + 1 + 8m = {m^2} + 6m + 1\) suy ra \(T = f\left( m \right) = {m^2} + 6m + 1\).
BBT:
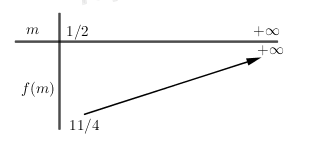
Dựa vào BBT của \(f\left( m \right)\) trên \(\left[ {\dfrac{1}{2}; + \infty } \right)\) ta tìm được GTNN của T bằng \(\dfrac{{11}}{4}\) khi \(m = \dfrac{1}{2}\).
Vậy \({T_{\min }} = \dfrac{{11}}{4} \Leftrightarrow m = \dfrac{1}{2}\).
