Cho tam giác ABC vuông tại A đường cao AH biết AC = 16cm và sin góc CAH = 45. Tính độ dài các cạnh

Câu hỏi
Nhận biếtCho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH,\) biết \(AC = 16cm\) và \(\sin \widehat {CAH} = \frac{4}{5}.\) Tính độ dài các cạnh \(BC,\;AB.\)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
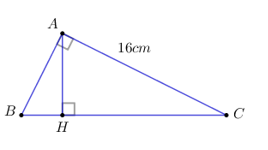
Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH,\) biết \(AC = 16cm\) và \(\sin \widehat {CAH} = \frac{4}{5}.\) Tính độ dài các cạnh \(BC,\;AB.\)
Xét tam giác \(CAH\) vuông tại \(H\) ta có:
\(\sin \widehat {CAH} = \frac{4}{5} \Leftrightarrow \frac{{HC}}{{AC}} = \frac{{HC}}{{16}} = \frac{4}{5} \Leftrightarrow HC = \frac{{4.16}}{5} = 12,8cm.\)
Áp dụng hệ thức lượng cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH\) ta có:
\(A{C^2} = HC.BC \Rightarrow BC = \frac{{A{C^2}}}{{HC}} = \frac{{{{16}^2}}}{{12,8}} = 20\left( {cm} \right)\)
Áp dụng định lý Pi-ta-go trong tam giác vuông ABC ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} \Rightarrow A{B^2} = B{C^2} - A{C^2} = {20^2} - {16^2} = 144\\ \Rightarrow AB = 12\left( {cm} \right)\end{array}\)
Vậy BC = 20 cm; AB = 12 cm.

