Cho abcd là các số dương thỏa mãn a2 + b2 = 1 và <

Câu hỏi
Nhận biếtCho a,b,c,d là các số dương thỏa mãn a2 + b2 = 1 và 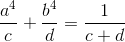
Chứng minh rằng 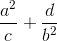 ≥ 2
≥ 2
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
a2 + b2 = 1 và 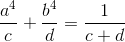
=> 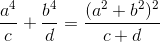
<=> d(c + d) a4 + c(c + d) b4 = cd (a2 + b2)2
<=> dca4 + d2a4 + c2b4 + c d b4 = cd (a4 + b4 + 2a2 b2)
<=> d2 a4 + c2 b4 – 2c da2 b2 = 0
<=> (da2 – cb2 )2 = 0
<=> da2 – cb2 = 0 hay 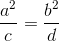
Do đó 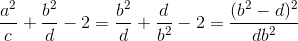 ≥ 0
≥ 0
Vậy 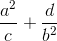 ≥ 2
≥ 2

