Tìm tất cả các số nguyên dương (x;y;z) thỏa mãn <

Câu hỏi
Nhận biếtTìm tất cả các số nguyên dương (x;y;z) thỏa mãn 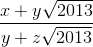 là số hữu tỷ, đồng thời x2 + y2 + z2 là số nguyên tố
là số hữu tỷ, đồng thời x2 + y2 + z2 là số nguyên tố
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Ta có 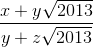 =
=  (m,n ∈ N*,(m,n) = 1)
(m,n ∈ N*,(m,n) = 1)
⇔ mx - my = (mz - ny)√ 2013 => 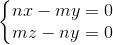 =>
=>  =
=  =
= 
=> xz = y2
.X2 + y2 + z2 = (x + z)2 – 2xz + y2 = (x + z)2 – y2
= (x + y + z)(x + z – y)
Vì x + y + z > 1 và x2 + y2 + z2 là các số nguyên tố nên 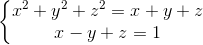
Suy ra x = y = z = 1 (thỏa mãn)

