Giải phương trình : (3x2 – 6x)(<
Câu hỏi
Nhận biếtGiải phương trình : (3x2 – 6x)(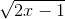
+ 1) = 2x3 – 5x2 + 4x - 4
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
(3x2 – 6x)(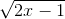
+ 1) = 2x3 – 5x2 + 4x - 4
⇔ 3x(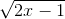 + 1) - x(2x - 1) - 2 = 0 (2)
Đặt 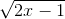= t với t ≥ 0 suy ra x = 
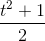thay vào phương trình (2) ta được
t4 – 3t3 – 2t2 – 3t + 1 = 0 ⇔ (t2 + t + 1)(t2 – 4t + 1) = 0
⇔ t2 – 4t + 1 = 0 ⇔ t = 2 ±√3
Từ đó tìm được x = 4 ±√3 (tm)
Vậy phương trình đã cho có 3 nghiệm x = 2 và x = 4 ±√3
