Cho biểu thức A = <
Câu hỏi
Nhận biếtCho biểu thức A =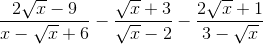 
a. Rút gọn A
b. Tìm các giá trị của x để A < 1
c. Tìm các giá trị nguyên của x để A nhận giá trị nguyên
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
a.
A =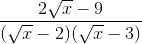 
- 
+ 
= 
= 
= 
= 
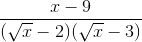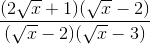
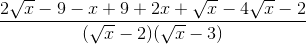
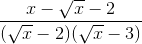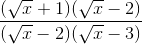
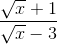( với x ≥ 0, x ≠ 4, x ≠ 9)
b.
A < 1 ⇔ 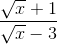< 1 ⇔ 
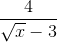< 0 ⇔ √x - 3 < 0
⇔ x < 9.
Kết hợp với điều kiện trên ta có, A < 1 khi 0 ≤ x < 9 và x ≠ 4
c.
A = 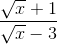= 1 +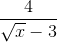
A nguyên khi và chỉ khi 4 chia hết cho √x - 3. Tức √x - 3 nhận các giá trị
± 1, ±2, ±4. Từ đó ta tìm được các giá trị nguyên của x là 1, 4, 16, 25, 49
