Một ô tô xuất phát từ điểm A trên cách đồng để đến điểm B trên sân vận động như hình vẽ. Cánh đồng v

Câu hỏi
Nhận biếtMột ô tô xuất phát từ điểm A trên cách đồng để đến điểm B trên sân vận động như hình vẽ. Cánh đồng và sân vận động được ngăn cách nhau bởi con đường thẳng D, khoảng cách từ A đến đường D là a = 400 m, khoảng cách từ B đến đường D là b = 300 m, khoảng cách AB = 2,8 km. Biết tốc độ của ô tô trên cách đồng là v = 3 km/h, trên đường D là 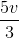 , trên sân vận động là
, trên sân vận động là 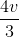 . Hỏi ô tô phải đi đến điểm M trên đường cách A’ một khoảng x và rời đường tại N cách B’ một khoảng y bằng bao nhiêu để thời gian chuyển động là nhỏ nhất? Xác định khoảng thời gian nhỏ nhất đó?
. Hỏi ô tô phải đi đến điểm M trên đường cách A’ một khoảng x và rời đường tại N cách B’ một khoảng y bằng bao nhiêu để thời gian chuyển động là nhỏ nhất? Xác định khoảng thời gian nhỏ nhất đó?

Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Xét hai tam giác vuông AOA’ ∽ BOB’ => 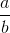 =
= 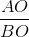 =>
=> 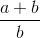 =
= 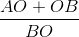
=> 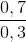 =
= 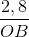 => OB = 1,2 km; OA = 1,6 km
=> OB = 1,2 km; OA = 1,6 km
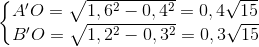 => A'B' = 0,7
=> A'B' = 0,7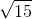 km
km
Giả sử người phải đi theo hướng AMNB. Đặt A'M = x, B'N = y, A'B' = c
=> điều kiện 0 ≤ x, y và ( x+ y ) ≤ c.
Thời hian đi theo AMNB là:
T = 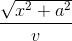 +
+ 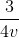 .
.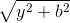 +
+ 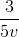 ( c - x - y ) ( với v = 3 km/h )
( c - x - y ) ( với v = 3 km/h )
Đặt Px = 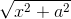 -
-  (1)
(1)
Qy = 
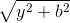 -
- 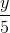 (2)
(2)
Ta có: T = 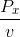 +
+ 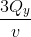 +
+ 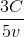 (3)
(3)
Từ (3) ta thấy để Tmin thì Px min và Qy min
(1) => P +  =
= 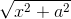 ( P ≥ 0; x ≥ 0 )
( P ≥ 0; x ≥ 0 )
=> 16x2 – 30Px + 25( a2 – P2 ) =0 (4)
Để (4) có nghiệm thì ∆' ≥ 0 <=> ∆' = 225P2 – 12.25( a2 – P2 ) ≥ 0
Hay P2 ≥ 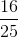 a2 => pmin =
a2 => pmin =  a (5)
a (5)
Giá trị của Pmin ứng với nghiệm kép của (4): x = 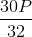 =
= 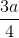
Tương tự ta có: Qmin = 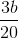 => y =
=> y = 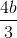 (6)
(6)
Thay (5), (6) vào (3) ta được: Tmin = 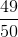 +
+ 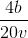 +
+ 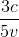
=> Tmin = 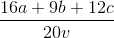
Thay số ta có x = 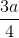 = 0,3 km = 300 m, y =
= 0,3 km = 300 m, y = 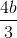 = 0,4 km = 400m, Tmin = 41 phút 38 giây
= 0,4 km = 400m, Tmin = 41 phút 38 giây








