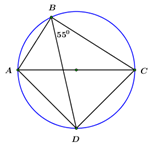
Cho tứ giác ABCD nội tiếp đường tròn đường kính AC. Biết angle DBC = 55^0 số đo angle ACD bằng:

Câu hỏi
Nhận biếtCho tứ giác \(ABCD\) nội tiếp đường tròn đường kính \(AC.\) Biết \(\angle DBC = {55^0},\) số đo \(\angle ACD\) bằng:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Ta có: \(\angle DBC = {55^0}\) là góc nội tiếp chắn cung \(DC \Rightarrow sd\,\,cung\,\,DC = 2.55 = {110^0}.\)
Vì \(AC\) là đường kính của đường tròn \( \Rightarrow sd\,\,cung\,\,AC = {180^0}.\)
\( \Rightarrow sd\,\,cung\,\,AD = sd\,\,cung\,\,AC - sd\,\,cung\,\,DC = {180^0} - {110^0} = {70^0}.\)
Ta có: \(\angle ACD\) là góc nội tiếp chắn cung nhỏ \(AD.\)
\( \Rightarrow \angle ACD = \frac{1}{2}sd\,\,cung\,\,AD = \frac{1}{2}{.70^0} = {35^0}.\)
Chọn D.