Trong mặt phẳng tọa độ Oxy cho đường tròn ( C ):x^2 + y^2 - 2x - 4y - 25 = 0 và điểm M( 2;1 ). Dây c

Câu hỏi
Nhận biếtTrong mặt phẳng tọa độ \(Oxy\), cho đường tròn \(\left( C \right):{x^2} + {y^2} - 2x - 4y - 25 = 0\) và điểm \(M\left( {2;1} \right)\). Dây cung của \(\left( C \right)\) đi qua \(M\left( {2;1} \right)\) có độ dài ngắn nhất là:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
+) Xét đường tròn \(\left( C \right):{x^2} + {y^2} - 2x - 4y - 25 = 0\), ta có:
- Tâm \(I\left( {1;2} \right)\)
- Bán kính \(R = \sqrt {{1^2} + {2^2} + 25} = \sqrt {30} \)
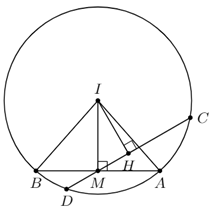
+) Giả sử, dây cung \(AB\) của đường tròn \(\left( C \right)\) đi qua \(M\) và vuông góc với \(IM\), \(CD\) là dây cung tùy ý đi qua \(M\) và \(IH \bot CD\)
Xét \(\Delta IMH\) vuông tại \(H\) ta có: \(IM \ge IH\) (trong tam giác vuông cạnh huyền là cạnh lớn nhất)
Xét đường tròn \(\left( C \right)\) có tâm \(I\left( {1;2} \right)\):
- \(IM\) là khoảng cách từ tâm \(I\) đến dây cung \(AB\)
- \(IH\) là khoảng cách từ tâm \(I\) đến dây cung \(CD\)
Vì \(IM \ge IH \Rightarrow AB \le CD\) (Khoảng cách từ tâm đến dây cung càng lớn thì dây cung càng nhỏ)
\( \Rightarrow \) \(AB\) là dây cung đi qua \(M\) có độ dài ngắn nhất.
\(IM = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {1 - 2} \right)}^2}} = \sqrt {1 + 1} = \sqrt 2 \)
Xét \(\Delta IMA\) vuông tại \(M\), áp dụng định lý Py-ta-go ta có:
\(I{M^2} + M{A^2} = I{A^2} \Rightarrow MA = \sqrt {I{A^2} - I{M^2}} = \sqrt {{{\left( {\sqrt {30} } \right)}^2} - {{\left( {\sqrt 2 } \right)}^2}} = \sqrt {30 - 2} = \sqrt {28} = 2\sqrt 7 \)
Vì \(IM \bot AB\) tại \(M\) nên \(M\) là trung điểm của \(AB\)\( \Rightarrow AB = 2MA = 2.2\sqrt 7 = 4\sqrt 7 \)
Vậy dây cung của \(\left( C \right)\) đi qua \(M\) có độ dài ngắn nhất bằng \(4\sqrt 7 .\)
Chọn B
