Cho hình thang vuông ABCD angle A = angle D = 90^0 có AB = AD = 2aDC = 6a. Với N là trung điểm BC t

Câu hỏi
Nhận biếtCho hình thang vuông ABCD, \(\angle A = \angle D = {90^0}\) có \(AB = AD = 2a,DC = 6a.\) Với \(N\) là trung điểm \(BC,\) tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {DN} ?\)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
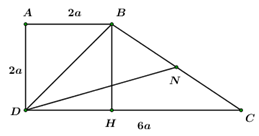
Kẻ \(BH \bot CD\) tại \(H \Rightarrow ABHD\) là hình vuông \( \Rightarrow BD = 2\sqrt 2 a.\)
\(\begin{array}{l}HC = 6a - 2a = 4a \Rightarrow BC = \sqrt {B{H^2} + H{C^2}} = \sqrt {4{a^2} + 16{a^2}} = 2a\sqrt 5 .\\\overrightarrow {AB} .\overrightarrow {DN} = \overrightarrow {AB} .\left( {\overrightarrow {DB} + \overrightarrow {BN} } \right) = \overrightarrow {AB} .\overrightarrow {DB} + \overrightarrow {AB} .\overrightarrow {BN} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = AB.DB.\cos \angle ABD + AB.BN.\cos .\left( {180^\circ - \angle ABN} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = AB.DB.\cos \angle ABD + AB.BN.\cos \angle BCD\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2a.2\sqrt 2 a.\frac{1}{{\sqrt 2 }} + 2a.2a\sqrt 5 .\frac{{4a}}{{2a\sqrt 5 }} = 12{a^2}.\end{array}\)
Chọn C.
