Tìm các nghiệm nguyên của phương trình x^2 - 2x - 11 = y^2.

Câu hỏi
Nhận biếtTìm các nghiệm nguyên của phương trình \({x^2} - 2x - 11 = {y^2}\).
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
\(\begin{array}{l}{x^2} - 2x - 11 = {y^2} \Leftrightarrow \left( {{x^2} - 2x + 1} \right) - {y^2} = 12\\ \Leftrightarrow {\left( {x - 1} \right)^2} - {y^2} = 12 \Leftrightarrow \left( {x - 1 - y} \right)\left( {x - 1 + y} \right) = 12\end{array}\)
Do \(x,\,\,y \in \mathbb{Z}\) nên \(x - 1 + y\) và \(x - 1 - y\) phải là ước của 12.
Ta có \(\left( {x - 1 - y} \right) + \left( {x - 1 + y} \right) = 2\left( {x - 1} \right)\) là số chẵn nên \(x - 1 + y\) và \(x - 1 - y\) cùng tính chẵn lẻ.
Mà tích của chúng bằng 12 là số chẵn nên \(x - 1 + y\) và \(x - 1 - y\) phải cùng chẵn.
Ta có bảng sau:
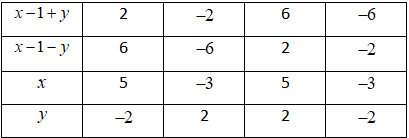
Vậy các nghiệm nguyên của phương trình là \(\left( {5; - 2} \right);\,\,\left( { - 3;2} \right);\,\,\left( {5;2} \right);\,\,\left( { - 3; - 2} \right)\).
Chọn B.

