Cho abc là các số thực không âm thỏa mãn: a + b + c = 3. Chứng minh rằng: (a – 1)3 + (b – 1)3 + (c
Câu hỏi
Nhận biếtCho a,b,c là các số thực không âm thỏa mãn: a + b + c = 3. Chứng minh rằng:
(a – 1)3 + (b – 1)3 + (c – 1)3 = - 
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Ta có:
(a – 1)3 = a3 - 3a2 + 3a – 1 = a(a2 – 3a +3) - 1
= 
≥ 
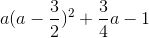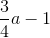(do a ≥ 0) (1)
Tương tự: (b – 1)3 ≥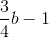 
(2)
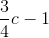(c – 1)3 ≥ 
(3)
Từ (1),(2),(3) suy ra:
(a – 1)3 + (b – 1)3 + (c – 1)3 ≥ 
(a + b + c) - 3 = 
- 3 =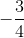 
Vậy bất đẳng thức được chứng minh.
Dấu đẳng thức xảy ra khi
<=> 
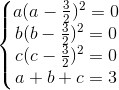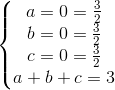
<=> a = 0, b = c = 
b = 0, a = c =
c = 0, a = b =
