Tìm m để hệ có nghiệm (x; y) thỏa mãn: x2 – 2y2 = 1

Câu hỏi
Nhận biếtTìm m để hệ có nghiệm (x; y) thỏa mãn: x2 – 2y2 = 1
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Giải hệ: 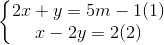 <=>
<=> 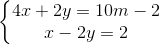
Cộng từng vế ta có: 5x = 10m => x = 2m
Thay vào phương trình (2) ta có:
2m - 2y = 2 => y = m - 1
Vậy hệ có nghiệm duy nhất: (x; y)= (2m; m -1).
Thay vào hệ thức: x2 – 2y2 = 1 ta có:
(2m)2 – 2(m – 1)2 = 1
<=> 4m2 – 2m2 + 4m – 2 – 1 = 0
<=> 2m2 + 4m – 3 = 0 (*)
(*) có ∆' = 22 – 2.(- 3) = 10 > 0
=> 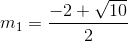 và
và 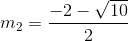
Vậy với 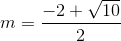 và
và 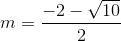 thì thỏa mãn hệ thức.
thì thỏa mãn hệ thức.

