Cho đường thẳng ( d1 ):y = 2x - 1 và đường thẳng ( d2 ):y = x + 1 a) Vẽ ( d1 ) và ( d2 ) trên cùng

Câu hỏi
Nhận biếtCho đường thẳng \(\left( {{d_1}} \right):y = 2x - 1\) và đường thẳng \(\left( {{d_2}} \right):y = x + 1\)
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép toán.
Tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ.
Ta có:
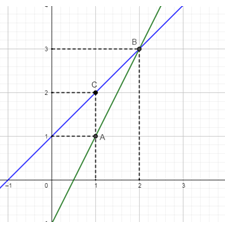
+) Hai điểm \(A\left( {1;1} \right),B\left( {2;3} \right)\) thuộc đồ thị hàm số \(\left( {{d_1}} \right):y = 2x - 1\)
+) Hai điểm \(B\left( {2;3} \right),C\left( {1;2} \right)\) thuộc đồ thị hàm số \(\left( {{d_2}} \right):y = x + 1\)
Từ đó ta có đồ thị của hai hàm số: (hình bên)
b)
Hoành độ giao điểm là nghiệm của phương trình:
\(2x - 1 = x + 1 \Leftrightarrow x = 2\)
Với \(x = 2 \Rightarrow y = x + 1 = 3\)
Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(B\left( {2;3} \right)\).
Chọn C

