Vẽ đồ thị của hai hàm số ứng với giá trị của m tìm được ở các câu 1) và 2) trên cùng hệ trục tọa độ

Câu hỏi
Nhận biếtVẽ đồ thị của hai hàm số ứng với giá trị của \(m\) tìm được ở các câu 1) và 2) trên cùng hệ trục tọa độ \(Oxy\) và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
+) Với \(m = 2\) hàm số trở thành \(y = x + 2\).
+) Với \(m = \frac{3}{2}\) hàm số trở thành \(y = \frac{1}{2}x + \frac{3}{2}\).
Ta có bảng giá trị:
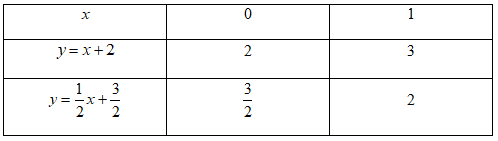
Đồ thị của hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \((1\,;\,\,3)\) và \((0\,;\,\,2)\).
Đồ thị của hàm số \(y = \frac{1}{2}x + \frac{3}{2}\) là đường thẳng đi qua hai điểm \(\left( {0\,;\,\,\frac{3}{2}} \right)\) và \((1\,;\,\,2)\).
+) Vẽ đồ thị của hai hàm số:
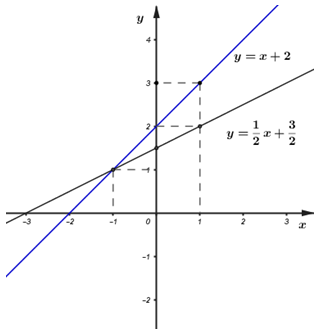
+) Tìm tọa độ giao điểm của hai đồ thị hàm số.
Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của phương trình:
\(\begin{array}{l}\;\;\;\;x + 2 = \frac{1}{2}x + \frac{3}{2} \Leftrightarrow x - \frac{1}{2}x = \frac{3}{2} - 2\\ \Leftrightarrow \frac{1}{2}x = \frac{{ - 1}}{2} \Leftrightarrow x = - 1\end{array}\)
Với \(x = - 1\) ta được \(y = - 1 + 2 = 1\).
Vậy tọa độ giao điểm của hai đường thẳng là \(( - 1\,;\,\,1)\).
Chọn C.

