Cho tam giác nhọn ABC (AB < AC) nội tiếp (O R). Các đường cao AD BE CF của tam giác ABC cắt nhau tạ

Câu hỏi
Nhận biếtCho tam giác nhọn ABC (AB < AC) nội tiếp (O, R). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Gọi M là trung điểm của BC.
a) Chứng minh tứ giác BFHD nội tiếp một đường tròn.
b) Biết: \(\angle EBC={{30}^{0}}.\) Tính \(\angle EMC.\)
c) Chứng minh: \(\angle FDE=\angle FME.\)
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
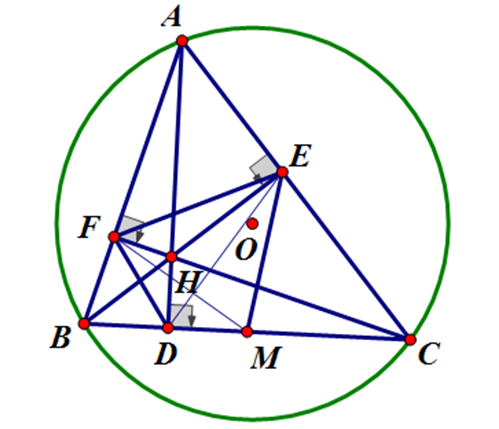
Cho tam giác nhọn ABC (AB < AC) nội tiếp (O, R). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Gọi M là trung điểm của BC.
a) Chứng minh tứ giác BFHD nội tiếp một đường tròn.
Ta có \(\angle BFH=\angle BDH={{90}^{0}}\Rightarrow \angle BFH+\angle BDH={{180}^{0}}\)
\(\Rightarrow \) Tứ giác BFHD nội tiếp (đpcm).
b) Biết: \(\angle EBC={{30}^{0}}.\) Tính \(\angle EMC.\)
Ta có: \(\Delta BEC\) là tam giác vuông tại \(E\) có đường trung tuyến \(EM\Rightarrow EM=BM=MC=\frac{BC}{2}.\)
\(\Rightarrow BME\) là tam giác cân tại \(M\Rightarrow \angle MBE=\angle BEM={{30}^{0}}.\)
\(\Rightarrow \angle EMC=\angle MBE+\angle BEM={{30}^{0}}+{{30}^{0}}={{60}^{0}}\) (góc ngoài của tam giác BME).
c) Chứng minh: \(\angle FDE=\angle FME.\)
Ta có \(\angle HDC+\angle HEC={{90}^{0}}+{{90}^{0}}={{180}^{0}}\Rightarrow DHEC\) là tứ giác nội tiếp.
Tứ giác \(BFEC\) có \(\angle BFC=\angle BEC={{90}^{0}}\)
Mà hai đỉnh \(E,\ F\) cùng kề cạnh \(EF\) nhìn cạnh \(BC\) dưới các góc bằng nhau và \(={{90}^{0}}\)
\(\Rightarrow BFEC\) là tứ giác nội tiếp.
\(\Rightarrow \angle FBE=\angle FCE\) (hai góc nội tiếp cùng chắn cung EH).
Vì tứ giác BDHF nội tiếp \(\Rightarrow \angle FBH=\angle FDH\) (hai góc nội tiếp cùng chắn cung FH).
Tứ giác DCEH nội tiếp \(\Rightarrow \angle EDH=\angle ECH\) (hai góc nội tiếp cùng chắn cung EH).
\(\Rightarrow \angle EDH=\angle FBH=\angle FCE=\angle HDE\Rightarrow \angle FDE=\angle FDH+\angle HDE=2.\angle FBE.\)
Mà \(\angle FBE\) là góc nội tiếp chắn cung EF còn \(\angle FME\) là góc ở tâm chắn cung EF
\(\angle FME=2\angle FBE\Rightarrow \angle FDE=2\angle FME.\)
Vậy ta có điều phải chứng minh.
Chọn B

