Từ điểm M nằm ở ngoài đường tròn ( OR ) với OM>2R vẽ hai tiếp tuyến MAMB AB là hai tiếp điểm). Gọi

Câu hỏi
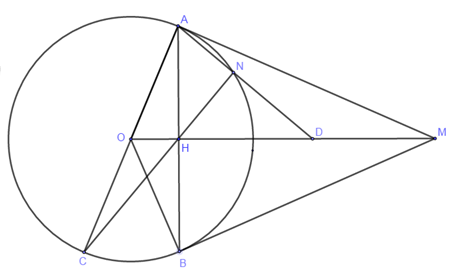
Nhận biếtTừ điểm \(M\) nằm ở ngoài đường tròn \(\left( O,R \right)\) với \(OM>2R\) vẽ hai tiếp tuyến \(MA,MB\) \(A,B\) là hai tiếp điểm). Gọi \(H\) là giao điểm của \(AB,OM\)
a) Nếu cho \(OM=R\sqrt{5}\) Tính độ dài đoạn \(MA\) theo \(R\) và số đo \(\angle AOM\) (làm tròn tới độ).
b) Chứng minh bốn điểm \(M,A,O,B\) thuộc một đường tròn.
c) Gọi \(AC\) là đường kính của đường tròn\(\left( O \right)\) tia \(CH\) cắt đường tròn \(\left( O \right)\) tại \(N\) Chứng minh \(4OH.OM=A{{C}^{2}}\)
d) Chứng minh rằng đường thẳng \(AN\) đi qua trung điểm của \(MH.\)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
a) Nếu cho \(OM=R\sqrt{5}\) Tính độ dài đoạn \(MA\) theo \(R\) và số đo \(\angle AOM\) (làm tròn tới độ)
Xét tam giác OAM vuông tại A có:
+) \(A{{M}^{2}}+O{{A}^{2}}=O{{M}^{2}}\Rightarrow AM=\sqrt{O{{M}^{2}}-O{{A}^{2}}}=\sqrt{{{\left( \sqrt{5}R \right)}^{2}}-{{R}^{2}}}=2R\) (định lí Py-ta-go)
+) \(\cos \left( \angle AOM \right)=\frac{OA}{OM}=\frac{R}{R\sqrt{5}}=\frac{1}{\sqrt{5}}\Rightarrow \angle AOM=\arccos \left( \frac{1}{\sqrt{5}} \right)\approx {{63}^{o}}\)
b) Chứng minh bốn điểm \(M,A,O,B\) thuộc một đường tròn.
Xét đường tròn \(\left( O,R \right)\) có: MA,MB là hai tiếp tuyến với A,B là tiếp điểm
\( \Rightarrow \left\{ \begin{array}{l}
OA \bot AM\\
OB \bot BM
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
\angle OAM = {90^o}\\
\angle OBM = {90^o}
\end{array} \right.\)
Xét tứ giác MAOB có: \(\angle OAM+\angle OBM={{90}^{o}}+{{90}^{o}}={{180}^{o}}\) suy ra tứ giác MAOB nội tiếp đường tròn, suy ra bốn điểm M, O, A, B cùng thuộc một đường tròn (đpcm).
c) Gọi \(AC\) là đường kính của đường tròn\(\left( O \right)\) tia \(CH\) cắt đường tròn \(\left( O \right)\) tại \(N\) Chứng minh: \(4OH.OM=A{{C}^{2}}\)
Có \(OA=OB\) (cùng là bán kính), suy ra O thuộc trung trực của AB.
Xét đường tròn \(\left( O,R \right)\) có: MA, MB là hai tiếp tuyến với A, B là tiếp điểm, suy ra \(MA=MB\) suy ra M thuộc trung trực của AB.
Từ hai điều trên ta được OM là trung trực của AB, suy ra OM vuông góc với AB tại H.
+) Xét tam giác vuông OAM vuông tại A có AH là đường cao
\(\Rightarrow O{{A}^{2}}=OH.OM\) (hệ thức lượng trong tam giác vuông)
+) Mà có: \(OA=\frac{1}{2}AC\) (do OA là bán kính, AC là đường kính)
\(\Rightarrow {{\left( \frac{1}{2}AC \right)}^{2}}=OH.OM\Rightarrow A{{C}^{2}}=4.OH.OM\) (đpcm).
d) Chứng minh rằng đường thẳng \(AN\) đi qua trung điểm của \(MH\)
Gọi D là giao điểm của AN và OM
Xét tam giác ADM và tam giác CHA có:
+) \(\angle ACN=\angle MAD\) ( góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AN )
+) \(\angle AMD=\angle CAH\) (do cùng phụ với \(\angle HAM\))
\(\Rightarrow \Delta ADM\sim \Delta CHA\ \ \left( g-g \right)\Rightarrow \frac{DM}{HA}=\frac{AD}{HC}\Rightarrow DM=AD.\frac{HA}{HC}\) (1)
Có AB vuông góc với OM (cmt) \(\Rightarrow \angle AHD={{90}^{o}}\)
Có \(\angle ANC\) là góc nội tiếp chắn nửa đường tròn \(\Rightarrow \angle ANC={{90}^{o}}\)
Xét hai tam giác vuông HDN và ADH có chung \(\angle NDH\)
\(\Rightarrow \Delta HDN\sim \Delta ADH\ \left( g-g \right)\Rightarrow \frac{HD}{AD}=\frac{HN}{AH}\Rightarrow HD=AD.\frac{HN}{AH}\) (2)
Xét tam giác AHC và tam giác NHB có:
+) \(\angle AHC=\angle NHB\) (hai góc đối đỉnh)
+) \(\angle CAH=\angle HNB\) (hai góc nội tiếp cùng chắn cung BC )
\(\Rightarrow \Delta AHC\sim \Delta NHB\ \ \left( g-g \right)\Rightarrow \frac{HN}{HA}=\frac{HB}{HC}\)
Mà có: \(HA=HB\) (do OM là trung trực của AB) \(\Rightarrow \frac{HN}{HA}=\frac{HA}{HC}\) (3)
Từ (1) , (2) , (3) suy ra \(HD=DM\) suy ra D là trung điểm của HM, suy ra AN đi qua trung điểm của HM (đpcm).
Chọn C

