Cho đường tròn (O; R) và điểm M cố định nằm ngoài (O; R). Từ M kẻ các tiếp tuyến MA MB tới (O; R) (

Câu hỏi
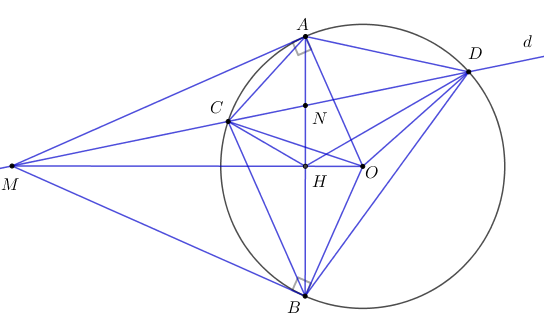
Nhận biếtCho đường tròn (O; R) và điểm M cố định nằm ngoài (O; R). Từ M kẻ các tiếp tuyến MA, MB tới (O; R) (A, B là các tiếp điểm). Đường thẳng (d) bất kỳ qua M và cắt (O; R) tại hai điểm phân biệt C, D (C nằm giữa M và D). Gọi N là giao điểm của AB và CD.
a) Chứng minh rằng tứ giác OAMB nội tiếp.
b) Chứng minh rằng \(\Delta ANC\) và \(\Delta DNB\) đồng dạng, \(\Delta AMC\) và \(\Delta DMA\) đồng dạng.
c) Chứng minh rằng:\(\frac{{MC}}{{MD}} = \frac{{NC}}{{ND}}.\)
d) Xác định vị trí của đường thẳng \(\left( d \right)\) để \(\frac{1}{{MD}} + \frac{1}{{ND}}\) đạt giá trị nhỏ nhất.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
a) Chứng minh rằng tứ giác OAMB nội tiếp.
Vì \(MA,\;\;MB\) là hai tiếp tuyến của \(\left( O \right) \Rightarrow \widehat {MAO} = \widehat {MBO} = {90^0}.\)
Xét tứ giác \(\widehat {MAO} + \widehat {OBM} = {90^0} + {90^0} = {180^0}\) \( \Rightarrow MAOB\) là tứ giác nội tiếp (dhnb).
b) Chứng minh rằng \(\Delta ANC\) và \(\Delta DNB\) đồng dạng, \(\Delta AMC\) và \(\Delta DMA\) đồng dạng.
Xét \(\Delta ANC\) và \(\Delta DNB\) ta có:
\(\widehat {CAN} = \widehat {NDB}\) (hai góc nội tiếp cùng chắn cung \(CB\))
\(\widehat {ANC} = \widehat {DNB}\) (hai góc đối đỉnh).
\( \Rightarrow \Delta ANC \sim \Delta DNB\;\left( {g - g} \right)\;\;\;\;\left( {dpcm} \right).\)
Xét \(\Delta AMC\) và \(\Delta DMA\) ta có:
\(\widehat {AMD}\;\;chung\)
\(\widehat {MAC} = \widehat {MDA}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AC\)).
\( \Rightarrow \Delta MAC \sim \Delta MDA\;\;\left( {g - g} \right)\;\;\;\left( {dpcm} \right).\)
c) Chứng minh rằng: \(\frac{{MC}}{{MD}} = \frac{{NC}}{{ND}}.\)
Ta có: \(\Delta MAC \sim \Delta MDA\;\;\left( {cmt} \right) \Rightarrow \frac{{MA}}{{MD}} = \frac{{MC}}{{MA}} \Leftrightarrow M{A^2} = MC.MD.\)
Gọi \(H\) là giao điểm của \(AB\) và \(MO \Rightarrow AB \bot MO = \left\{ H \right\}.\) (tính chất hai tiếp tuyến cắt nhau)
Xét tam giác \(MAO\) vuông tại \(A\) và có đường cao \(AH\) có:
\(M{A^2} = MH.MO.\) (hệ thức lượng trong tam giác vuông)
\(\begin{array}{l} \Rightarrow MC.MD = MH.MO\;\left( { = M{A^2}} \right).\\ \Rightarrow \frac{{MC}}{{MO}} = \frac{{MH}}{{MO}}.\end{array}\)
Xét \(\Delta MCH\) và \(\Delta MOD\) ta có:
\(\begin{array}{l}\frac{{MC}}{{MH}} = \frac{{MO}}{{MD}}\;\;\left( {cmt} \right)\\\widehat {OMD}\;\;chung\\ \Rightarrow \Delta MCH \sim \Delta MOD\;\;\left( {g - g} \right).\end{array}\)
\( \Rightarrow \widehat {MHC} = \widehat {MDO}\) (hai góc tương ứng).
Xét tứ giác \(CHOD\) ta có: \(\widehat {MHC} = \widehat {CDO}\;\;\left( {cmt} \right)\)
\( \Rightarrow CHOD\) là tứ giác nội tiếp. (góc ngoại tại một đỉnh bằng góc trong tại đỉnh đối diện)
\( \Rightarrow \widehat {DHO} = \widehat {DCO}\) (hai góc nội tiếp cùng chắn cung \(DO\))
Lại có: \(\widehat {ODC} = \widehat {OCD}\) \((\Delta COD\) cân tại \(O)\)
\( \Rightarrow \widehat {DHO} = \widehat {CHM}\left( { = \widehat {CDO}} \right).\)
Mà \(HM \bot HN\;\;\left( {cmt} \right)\)
\( \Rightarrow \widehat {NHC} = \widehat {NHD}\;\left( { = {{90}^0} - \widehat {CHM}} \right)\)
\( \Rightarrow NH\) là tia phân giác trong của \(\widehat {CHD}\) và \(HM\) là tia phân giác ngoài của \(\widehat {CHD}.\)
\( \Rightarrow \frac{{MC}}{{MD}} = \frac{{NC}}{{ND}}\left( { = \frac{{HC}}{{HD}}} \right).\;\;\left( {dpcm} \right)\)
d) Xác định vị trí của đường thẳng \(\left( d \right)\) để \(\frac{1}{{MD}} + \frac{1}{{ND}}\) đạt giá trị nhỏ nhất.
Xét: \(DC\left( {\frac{1}{{MD}} + \frac{1}{{ND}}} \right)\)
\(\begin{array}{l} = \frac{{CD}}{{MD}} + \frac{{CD}}{{ND}} = \frac{{MD - CM}}{{MD}} + \frac{{CN + ND}}{{ND}}\\ = 1 - \frac{{CM}}{{MD}} + 1 + \frac{{CN}}{{ND}} = 2 + \frac{{CN}}{{DN}} - \frac{{MC}}{{MD}} = 2.\;\;\;\left( {do\;\;\frac{{MC}}{{MD}} = \frac{{NC}}{{ND}}} \right)\\ \Rightarrow \frac{1}{{MD}} + \frac{1}{{ND}} = \frac{2}{{CD}}.\end{array}\)
Vì \(CD\) là dây cung \( \Rightarrow CD \le 2R \Rightarrow \frac{2}{{CD}} \ge \frac{2}{{2R}} \Leftrightarrow \frac{2}{{CD}} \ge \frac{1}{R}.\)
\( \Rightarrow \frac{1}{{MD}} + \frac{1}{{ND}} \ge \frac{1}{R}.\)
Dấu “=” xảy ra \( \Leftrightarrow CD = 2R\) hay đường thẳng \(d\) đi qua \(O.\)
Vậy để \(\frac{1}{{MD}} + \frac{1}{{ND}}\) đạt giá trị nhỏ nhất thì đường thẳng \(d\) đi qua \(O.\)

