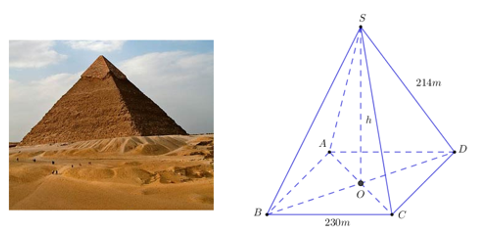
Kim tự tháp Kheops – Ai Cập có dạng hình chóp đều đáy là hình vuông các mặt bên là các tam giác cân

Câu hỏi
Nhận biếtKim tự tháp Kheops – Ai Cập có dạng hình chóp đều, đáy là hình vuông, các mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của kim tự tháp dài 214 m, cạnh đáy của nó dài 230 m.
a) Tính theo mét chiều cao h của kim tự tháp (làm tròn đến chữ số thập phân thứ nhất).
b) Cho biết thể tích của hình chóp được tính theo công thức \(V = \frac{1}{3}Sh\), trong đó \(S\) là diện tích mặt đáy, h là chiều cao của hình chóp. Tính theo \({m^3}\) thể tích của kim tự tháp (làm tròn đến hàng nghìn).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
a) Tính theo mét chiều cao h của kim tự tháp (làm tròn đến chữ số thập phân thứ nhất).
ABCD là hình vuông \( \Rightarrow \Delta ABD\) vuông cân tại A. Theo Py-ta-go, ta có:
\(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt 2 AB = 230\sqrt 2 \,(m)\)
ABCD là hình vuông \( \Rightarrow O\)là trung điểm của BD \( \Rightarrow OB = \frac{{BD}}{2} = \frac{{230\sqrt 2 }}{2} = 115\sqrt 2 \,\,(m)\)
\(\Delta SOB\) vuông tại O , theo Py-ta-go, ta có:
\(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {{{214}^2} - {{\left( {115\sqrt 2 } \right)}^2}} \approx 139,1\,\,(m) \Rightarrow h \approx 139,1\,\,(m)\).
b) Cho biết thể tích của hình chóp được tính theo công thức \(V = \frac{1}{3}Sh\), trong đó \(S\) là diện tích mặt đáy, h là chiều cao của hình chóp. Tính theo \({m^3}\) thể tích của kim tự tháp (làm tròn đến hàng nghìn).
Diện tích đáy là: \(S = {S_{ABCD}} = C{D^2} = {230^2}\,\,({m^2})\)
Thể tích của hình chóp là: \(V = \frac{1}{3}Sh \approx \frac{1}{3}{.230^2}.139,1 \approx 2452796,667 \approx 2453000\,\,({m^3})\).