Chứng minh rằng trong 10 số nguyên dương liên tiếp không tồn
Câu hỏi
Nhận biếtChứng minh rằng trong 10 số nguyên dương liên tiếp không tồn tại hai số có ước chung lớn hơn 9.
Đáp án đúng: B
Lời giải của Tự Học 365
Cách giải nhanh bài tập này
Gọi 10 số nguyên dương liên tiếp là: n, n+1, n+2, ..., n+9 ( n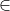 
N*).
Giả sử tồn tại 2 số trong 10 số này có ước chung lớn hơn 9 là d (d 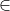N, d>9) và hai số đó là n+a, n+b 
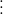d
Do đó n+a 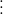d và n+b 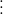d => (n+a) - (n+b) 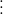9
=> a-b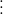 d. Vì 0< a-b 
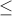9. Nên d 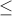9
Ta có d > 9. Điều này mâu thuẫn!
Như vậy điều giả sử ở trên là sai.
Vậy trong 10 số nguyên dương liên tiếp không tồn tại hai số có ước chung lớn hơn 9.
